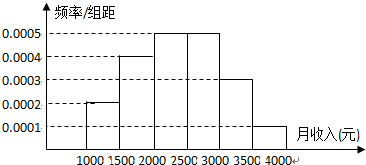
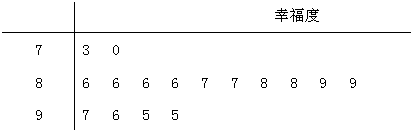
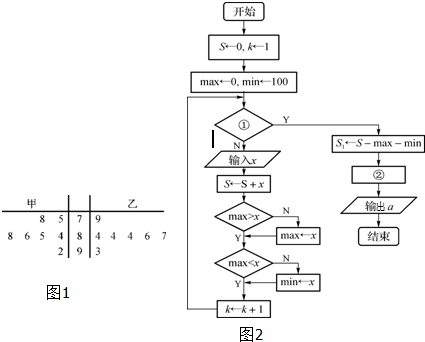
题目内容
从1,3,5,7,9五个数字中选2个,0,2,4,6,8五个数字中选2个,能组成多少个无重复数字的四位偶数?
考点:计数原理的应用
专题:排列组合
分析:根据分类计数原理,因为0是偶数且不能排在首位,所以要以选0和不选0分为两类,再按其他要求排列.
解答:
解:分类:第一类:选0,四位偶数有
)=400个;
第二类:不选0,四位偶数有
=720个;
所以,共能组成400+720=1120个无重复数字的四位偶数.
| C | 2 5 |
| •C | 1 4 |
| (A | 3 3 |
| +A | 1 2 |
| •A | 2 2 |
第二类:不选0,四位偶数有
| C | 2 5 |
| •C | 2 4 |
| •A | 1 2 |
| •A | 3 3 |
所以,共能组成400+720=1120个无重复数字的四位偶数.
点评:本题主要考查了分类计数原理,分清特殊元素是分类的关键,属于中档题.

练习册系列答案
相关题目