Question

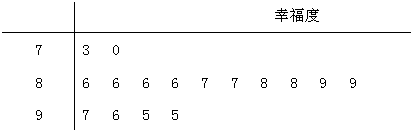
某校学生会组织部分同学用“10分制”随机调查“阳光”社区人们的幸福度，现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）．
（Ⅰ）指出这组数据的众数和中位数；
（Ⅱ）若幸福度不低于9.5分，则该人的幸福度为“很幸福”，按分层抽样的方法从16人中抽取8人，并从8人中随机抽取2人，求2人中至少有1人“很幸福”的概率．

Answer 1

考点：茎叶图,众数、中位数、平均数

专题：计算题,概率与统计

分析：（I）根据众数是出现次数最多的数求出众数；根据中位数是从小到大排列位于中间位置的两数的平均数求中位数；
（II）由茎叶图求出幸福度不低于9.5分的人数，计算按分层抽样的方法从幸福度不低于9.5分的应抽取是人数，
再分别求出从8人中随机抽取2人的抽法种数和2人中至少有1人“很幸福”的抽法种数，利用古典概型概率公式计算．

解答： 解：（Ⅰ）由茎叶图知：众数为8.6；    中位数为8.75；
（Ⅱ）设A表示“2个人中至少有一个人‘很幸福’”这一事件
由茎叶图知：幸福度不低于9.5分的有4人，
∴按分层抽样的方法从16人中抽取8人，其中幸福度不低于9.5分的应抽取2人，
从8人中随机抽取2人，所有可能的结果有

C

2 8

=28个，
其中事件A中的可能性有 

C

2 2

+

C

1 2

×C

1 6

=13个，
∴概率P（A）=

13

28

．

点评：本题考查了由茎叶图求数据的众数、中位数，考查了古典概型的概率计算及组合数公式的应用，是概率统计的基本题型，读懂茎叶图是解题的关键．