题目内容
如果椭圆
+
=1上任意两点连线的垂直平分线与x轴相交于点P(x0,0),求x0的取值范围.
| x2 |
| 16 |
| y2 |
| 4 |
考点:椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:对直线AB的斜率分类讨论,当直线AB的斜率存在且不为0时,设斜率为k,设直线AB的方程为y=kx+m.与椭圆方程联立得到△>0即根与系数的关系,再利用中点坐标公式即可得出线段AB的中点,进而得出垂直平分线的方程,即可得出.
解答:
解:设椭圆
+
=1上任意两点为A,B,则
①当AB∥x轴或与x轴重合时,此时kAB=0,线段AB的垂直平分线与x轴交于点P(0,0);
②当AB⊥x轴时,此时线段AB的垂直平分线为x轴,此时不符合题意,应舍去;
③当直线AB的斜率存在且不为0时,设斜率为k,设直线AB的方程为y=kx+m.A(x1,y1),B(x2,y2)
代入椭圆
+
=1,化为(1+4k2)x2+8kmx+4m2-16=0,
∵△=64k2m2-4(1+4k2)(4m2-16)>0,化为-m2+4+16k2>0(*).
∴x1+x2=-
.
设线段AB的中点为M(xM,yM).则xM=-
,yM=kxM+m=
.
线段AB的垂直平分线的方程为y=-
(x-x0),
把点M的坐标代入可得
=-
(-
-x0),
∴m=-
,代入(*)得x02<
.
令f(k)=
=
,则0<f(k)<9
∴x02<9.
∴-3<x0<3.
综上可知:x0的取值范围是(-3,3).
| x2 |
| 16 |
| y2 |
| 4 |
①当AB∥x轴或与x轴重合时,此时kAB=0,线段AB的垂直平分线与x轴交于点P(0,0);
②当AB⊥x轴时,此时线段AB的垂直平分线为x轴,此时不符合题意,应舍去;
③当直线AB的斜率存在且不为0时,设斜率为k,设直线AB的方程为y=kx+m.A(x1,y1),B(x2,y2)
代入椭圆
| x2 |
| 16 |
| y2 |
| 4 |
∵△=64k2m2-4(1+4k2)(4m2-16)>0,化为-m2+4+16k2>0(*).
∴x1+x2=-
| 8km |
| 1+4k2 |
设线段AB的中点为M(xM,yM).则xM=-
| 4km |
| 1+4k2 |
| m |
| 1+4k2 |
线段AB的垂直平分线的方程为y=-
| 1 |
| k |
把点M的坐标代入可得
| m |
| 1+4k2 |
| 1 |
| k |
| 4km |
| 1+4k2 |
∴m=-
| x0(1+4k2) |
| 3k |
| 36k2 |
| 1+4k2 |
令f(k)=
| 36k2 |
| 1+4k2 |
| 36 | ||
|
∴x02<9.
∴-3<x0<3.
综上可知:x0的取值范围是(-3,3).
点评:熟练掌握椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到△>0及根与系数的关系、中点坐标公式、垂直平分线的性质、点到直线的距离公式等是解题的关键.

练习册系列答案
相关题目
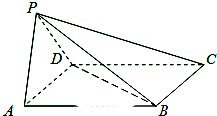 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠BAD=45°,AD=1,AB=
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠BAD=45°,AD=1,AB= 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:请观察图形,求解下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:请观察图形,求解下列问题: