题目内容
在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:2x+y=0(x≥0),过点P(1,0)作直线分别交射线OA、OB于点C、D.
(1)当△COP的面积等于△DOP面积时,求直线CD的方程;
(2)当CD的中点在直线x-2y=0上时,求直线CD的方程.
(1)当△COP的面积等于△DOP面积时,求直线CD的方程;
(2)当CD的中点在直线x-2y=0上时,求直线CD的方程.
考点:直线的截距式方程
专题:直线与圆
分析:设直线CD的方程为:y=k(x-1),设C(x1,y1),D(x2,y2),由已知条件解得
,
,
(1)由△COP的面积等于△DOP面积,知y1=-y2,由此能求出直线CD的方程.
(2)CD的中点坐标为(
(
+
),
(
-
))=(
,
),由CD的中点在直线x-2y=0上,得
-
=0,由此能求出直线CD的方程.
|
|
(1)由△COP的面积等于△DOP面积,知y1=-y2,由此能求出直线CD的方程.
(2)CD的中点坐标为(
| 1 |
| 2 |
| k |
| k-1 |
| k |
| k+2 |
| 1 |
| 2 |
| k |
| k-1 |
| 2k |
| k+2 |
k2-
| ||
| (k-1)(k+2) |
2k-
| ||
| (k-1)(k+2) |
k2-
| ||
| (k-1)(k+2) |
| 4k-k2 |
| (k-1)(k+2) |
解答:
解:(1)设直线CD的方程为:y=k(x-1),
设C(x1,y1),D(x2,y2),
由
,得
,
由
,得
,
∵△COP的面积等于△DOP面积,
∴y1=-y2,即
=
,
解得k=4或k=0(舍),
∴直线CD的方程为:y=4(x-1),即4x-y-4=0.
(2)设直线CD的方程为:y=k(x-1),
设C(x1,y1),D(x2,y2),
由
,得
,
由
,得
,
∴CD的中点坐标为(
(
+
),
(
-
))=(
,
),
∵CD的中点在直线x-2y=0上,
∴
-
=0,
解得k=18或k=0(舍),
∴直线CD的方程为y=18(x-1),即18x-y-18=0.
设C(x1,y1),D(x2,y2),
由
|
|
由
|
|
∵△COP的面积等于△DOP面积,
∴y1=-y2,即
| k |
| k-1 |
| 2k |
| k+2 |
解得k=4或k=0(舍),
∴直线CD的方程为:y=4(x-1),即4x-y-4=0.
(2)设直线CD的方程为:y=k(x-1),
设C(x1,y1),D(x2,y2),
由
|
|
由
|
|
∴CD的中点坐标为(
| 1 |
| 2 |
| k |
| k-1 |
| k |
| k+2 |
| 1 |
| 2 |
| k |
| k-1 |
| 2k |
| k+2 |
k2-
| ||
| (k-1)(k+2) |
2k-
| ||
| (k-1)(k+2) |
∵CD的中点在直线x-2y=0上,
∴
k2-
| ||
| (k-1)(k+2) |
| 4k-k2 |
| (k-1)(k+2) |
解得k=18或k=0(舍),
∴直线CD的方程为y=18(x-1),即18x-y-18=0.
点评:本题考查直线方程的求法,是中档题时,解题时要认真[是题,注意中点坐标公式的合理运用.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
如果f(x+1)=
,f(1)=1(x∈N),猜想函数f(x)为( )
| 2f(x) |
| f(x)+2 |
A、f(x)=
| ||||
B、f(x)=
| ||||
| C、f(x)=x2+x-1 | ||||
D、f(x)=-
|
 如图,PD⊥平面ABC,AC=BC,D为AB的中点,E为AP的中点.
如图,PD⊥平面ABC,AC=BC,D为AB的中点,E为AP的中点.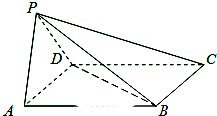 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠BAD=45°,AD=1,AB=
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠BAD=45°,AD=1,AB= 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:请观察图形,求解下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:请观察图形,求解下列问题: