题目内容
已知函数f(x)=
(其中常数a,b∈R).
(Ⅰ)当a=1时,若函数f(x)是奇函数,求f(x)的极值点;
(Ⅱ)求函数f(x)的单调递增区间.
| ax+b |
| x2+1 |
(Ⅰ)当a=1时,若函数f(x)是奇函数,求f(x)的极值点;
(Ⅱ)求函数f(x)的单调递增区间.
考点:利用导数研究函数的极值,函数单调性的判断与证明,利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:(Ⅰ)由函数f(x)是奇函数可得
=-
,从而解出b,代入求极值点;
(Ⅱ)求导f′(x)=
,则可化f′(x)=
>0为ax2+2bx-a<0;从而讨论a,b确定不等式ax2+2bx-a<0的解集即可.
| -x+b |
| x2+1 |
| x+b |
| x2+1 |
(Ⅱ)求导f′(x)=
| -ax2-2bx+a |
| (x2+1)2 |
| -ax2-2bx+a |
| (x2+1)2 |
解答:
解:(Ⅰ)∵函数f(x)是奇函数,
∴对x∈R,f(-x)=-f(x)成立,
∴
=-
,
∴2b=0,
∴b=0;
∴f(x)=
,得f′(x)=
;
令f′(x)=0得x=±1;
经检验x=-1是函数f(x)的极小值点,x=1是函数f(x)的极大值点.
(Ⅱ)∵f(x)=
,
∴f′(x)=
,
由f′(x)=
>0得ax2+2bx-a<0;
①当a=b=0时,f(x)=0,不存在单调递增区间;
②当a=0,b≠0时,
<ⅰ>b>0时,单调递增区间为(-∞,0);
<ⅱ>b<0时,单调递增区间为(0,+∞);
③当a>0时,方程ax2+2bx-a=0的两根x=
;
单调递增区间为(
,
);
④当a<0时,单调递增区间为(-∞,
)和(
,+∞).
∴对x∈R,f(-x)=-f(x)成立,
∴
| -x+b |
| x2+1 |
| x+b |
| x2+1 |
∴2b=0,
∴b=0;
∴f(x)=
| x |
| x2+1 |
| -x2+1 |
| (x2+1)2 |
令f′(x)=0得x=±1;
经检验x=-1是函数f(x)的极小值点,x=1是函数f(x)的极大值点.
(Ⅱ)∵f(x)=
| ax+b |
| x2+1 |
∴f′(x)=
| -ax2-2bx+a |
| (x2+1)2 |
由f′(x)=
| -ax2-2bx+a |
| (x2+1)2 |
①当a=b=0时,f(x)=0,不存在单调递增区间;
②当a=0,b≠0时,
<ⅰ>b>0时,单调递增区间为(-∞,0);
<ⅱ>b<0时,单调递增区间为(0,+∞);
③当a>0时,方程ax2+2bx-a=0的两根x=
-b±
| ||
| a |
单调递增区间为(
-b-
| ||
| a |
-b+
| ||
| a |
④当a<0时,单调递增区间为(-∞,
-b-
| ||
| a |
-b+
| ||
| a |
点评:本题考查函数、导数知识及其应用,考查运算求解能力,考查函数与方程思想、分类与整合思想、数形结合思想及化归与转化思想.属于难题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
在等差数列{an}中,a2=1,S5=15,则a4等于( )
| A、3 | B、5 | C、6 | D、8 |
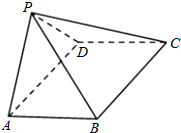 如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.