题目内容
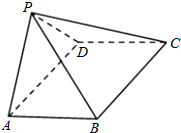 如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.(Ⅰ)求证:AB⊥PD;
(Ⅱ)若PA=PD=AB=2,问当AD为何值时,四棱锥P-ABCD的体积最大?并求其最大体积.
考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(Ⅰ)由已知得AB⊥面PAD,由此能证明AB⊥PD.
(Ⅱ)取AD中点O,连结PO,则PO⊥面ABCD,由此能推导出AD=2
时,Vmax=
.
(Ⅱ)取AD中点O,连结PO,则PO⊥面ABCD,由此能推导出AD=2
| 2 |
| 8 |
| 3 |
解答:
 (Ⅰ)证明:∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,AB⊥AD,
(Ⅰ)证明:∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,AB⊥AD,
∴AB⊥面PAD,
又∵PD?面PAD,
∴AB⊥PD.
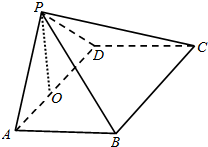
(Ⅱ)解:取AD中点O,连结PO,
∵PA=PD,∴PO⊥AD,
由(Ⅰ)有PO⊥面ABCD,
设AD=x.PO=
=
=
,
VP-ABCD=
×OP×S△ABCD
=
×2x×
=
.
=
,
∴当x2=8,即x=2
时,Vmax=
.
 (Ⅰ)证明:∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,AB⊥AD,
(Ⅰ)证明:∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,AB⊥AD,∴AB⊥面PAD,
又∵PD?面PAD,
∴AB⊥PD.
(Ⅱ)解:取AD中点O,连结PO,
∵PA=PD,∴PO⊥AD,
由(Ⅰ)有PO⊥面ABCD,
设AD=x.PO=
| AP2-AO2 |
4-
|
| 1 |
| 2 |
| 16-x2 |
VP-ABCD=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 16-x2 |
| 1 |
| 3 |
| 16x2-x4 |
=
| 1 |
| 3 |
| -(x2-8)2+64 |
∴当x2=8,即x=2
| 2 |
| 8 |
| 3 |
点评:本题考查异面直线垂直的证明,考查当AD为何值时,四棱锥P-ABCD的体积最大,并求其最大体积,解题时要注意空间思维能力的培养.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
定义在R上的函数f(x)满足:①对任意的x∈R,都有f(1+x)=f(1-x)成立;②对任意的x1,x2∈[1,+∞)且x1≠x2,都有
<0成立,则( )
| f(x1)-f(x2) |
| x1-x2 |
A、f(0)<f(
| ||
B、f(3)<f(
| ||
C、f(3)<f(0)<f(
| ||
D、f(0)<f(3)<f(
|
已知函数f(x)=
的定义域是一切实数,则m的取值范围是( )
| mx2+mx+1 |
| A、0<m≤4 | B、0≤m≤1 |
| C、m≥4 | D、0≤m≤4 |