题目内容
已知函数f(x)=cosx-
(x∈R,x≠0),则f′(1)值为( )
| 1 |
| x |
| A、-1-sin1 |
| B、1+sin1 |
| C、-1+sin1 |
| D、1-sin1 |
考点:导数的运算
专题:导数的概念及应用
分析:根据导数的运算法则,先求导,再带入求值.
解答:
解:∵f(x)=cosx-
,
∴f′(x)=-sinx+
,
∴f′(1)=-sin1+1,
故选:D.
| 1 |
| x |
∴f′(x)=-sinx+
| 1 |
| x2 |
∴f′(1)=-sin1+1,
故选:D.
点评:本题主要考查了常见函数的导数和导数的运算法则,属于基础题.

练习册系列答案
相关题目
已知x>0,n∈N*,由下列结论x+
≥2,x+
≥3,x+
≥4,…,得到一个正确的结论可以是( )
| 1 |
| x |
| 4 |
| x2 |
| 27 |
| x3 |
A、x+
| ||
B、x+
| ||
C、x+
| ||
D、x+
|
在样本的频率分布直方图中,共有8个小长方形,若最后一个小长方形的面积等于其它7个小长方形的面积和的
,且样本容量为200,则第8组的频数为( )
| 1 |
| 4 |
| A、40 | B、0.2 |
| C、50 | D、0.25 |
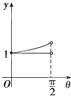
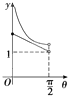
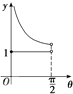
 如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,
如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,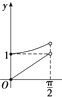
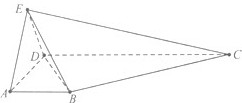 如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=
如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC= 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,AC=2,E为A1C!中点,求直线CC1与平面BCE所成角的大小.(结果用反三角函数值表示)
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,AC=2,E为A1C!中点,求直线CC1与平面BCE所成角的大小.(结果用反三角函数值表示)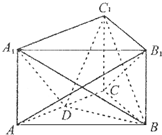 如图所示,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且底面是边长为2的正三角形,侧棱长为1,D是AC的中点.
如图所示,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且底面是边长为2的正三角形,侧棱长为1,D是AC的中点.