题目内容
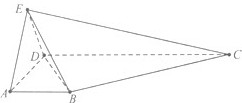 如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=
如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=| 13 |
(Ⅰ)求证:平面EAD⊥平面ABCD;
(Ⅱ)求二面角D-BE-C的余弦值.
考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)取AD的中点H,连结EH、CH,由已知条件得△ADE为正三角形,从而得到EH⊥AD,由勾股定理得EH⊥HC,所以EH⊥平面ABCD,由此能证明平面EAD⊥平面ABCD.
(Ⅱ)以H为坐标原点,建立如图所示的空间直角坐标系H-xyz,利用向量法能求出二面角D-BE-C的余弦值.
(Ⅱ)以H为坐标原点,建立如图所示的空间直角坐标系H-xyz,利用向量法能求出二面角D-BE-C的余弦值.
解答:
(Ⅰ)证明:取AD的中点H,连结EH、CH,
∵EA=AD=DE=2,∴△ADE为正三角形,
∴EH⊥AD,EH=3,
在Rt△HDC中,CD=3,DH=1,
∴HC=
=
,
在△EHC中,EH=
,HC=
,EC=
,
∴EC2=EH2+HC2,
∴∠EHC=90°,EH⊥HC,
又∵AD?平面ABCD,HC?平面ABCD,
AD∩HC=H,∴EH⊥平面ABCD,
又∵EH?平面EAD,
∴平面EAD⊥平面ABCD.
(Ⅱ)解:以H为坐标原点,建立如图所示的空间直角坐标系H-xyz,
则H(0,0,0),A(1,0,0),B(1,1,0),
D(-1,0,0),C(-1,3,0),E(0,0,
),
=(-2,-1,0),
=(-1,-1,
),
=(-2,2,0),
设平面DEB的法向量
=(x,y,z),
则
,取z=1,得
=(-
,2
,1),
设平面CBE的法向量
=(a,b,c),
则
,取a=
,得
=(
,
,2),
∴cos<
,
>=
=
.
∴二面角D-BE-C的余弦值为
.
∵EA=AD=DE=2,∴△ADE为正三角形,

∴EH⊥AD,EH=3,
在Rt△HDC中,CD=3,DH=1,
∴HC=
| 32+12 |
| 10 |
在△EHC中,EH=
| 3 |
| 10 |
| 13 |
∴EC2=EH2+HC2,
∴∠EHC=90°,EH⊥HC,
又∵AD?平面ABCD,HC?平面ABCD,
AD∩HC=H,∴EH⊥平面ABCD,
又∵EH?平面EAD,
∴平面EAD⊥平面ABCD.
(Ⅱ)解:以H为坐标原点,建立如图所示的空间直角坐标系H-xyz,
则H(0,0,0),A(1,0,0),B(1,1,0),

D(-1,0,0),C(-1,3,0),E(0,0,
| 3 |
| BD |
| BE |
| 3 |
| BC |
设平面DEB的法向量
| m |
则
|
| m |
| 3 |
| 3 |
设平面CBE的法向量
| n |
则
|
| 3 |
| n |
| 3 |
| 3 |
∴cos<
| m |
| n |
| 5 | ||
4
|
| ||
| 8 |
∴二面角D-BE-C的余弦值为
| ||
| 8 |
点评:本题考查平面与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知△ABC中,a=b=4,c=4
,则∠C=( )
| 3 |
| A、150° |
| B、30°或150° |
| C、120° |
| D、60°或120° |
甲乙两人通过考试的概率分别为
和
,两人同时参加考试,其中恰有一人通过的概率是( )
| 3 |
| 5 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知数列{an}为等比数列,且a1=1,a4=8,则公比q=( )
| A、1 | B、2 | C、4 | D、8 |
已知函数f(x)=cosx-
(x∈R,x≠0),则f′(1)值为( )
| 1 |
| x |
| A、-1-sin1 |
| B、1+sin1 |
| C、-1+sin1 |
| D、1-sin1 |
 如图,在平行四边形ABCD中,AB=2AD,∠BAD=60°,E为AB的中点,将△ADE沿直线DE折起到△PDE的位置,使平面PDE⊥平面BCDE.
如图,在平行四边形ABCD中,AB=2AD,∠BAD=60°,E为AB的中点,将△ADE沿直线DE折起到△PDE的位置,使平面PDE⊥平面BCDE.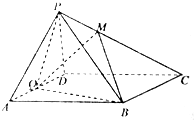 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,点Q为线段AD中点,PQ与QB不垂直.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,点Q为线段AD中点,PQ与QB不垂直.