题目内容
 如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,
如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,| π |
| 2 |
A、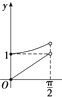 |
B、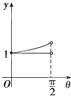 |
C、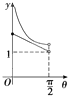 |
D、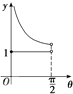 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:用特殊值法,当θ→0时,e1→2,e1e2=1,根据图象可得结论.
解答:
解:用特殊值法,当θ→0时,e1→2,e1e2=1,根据图象,D符合.
故选:D.
故选:D.
点评:本题主要考查椭圆和双曲线的离心率的表示,考查考生对圆锥曲线的性质的应用,圆锥曲线是高考的重点每年必考,平时要注意基础知识的积累和练习.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
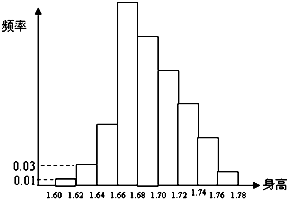 为了解某校身高在1.60m~1.78m的高一学生的情况,随机地抽查了该校100名高一学生,得到如图所示频率直方图.由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为m,身高在1.66m~1.74m的学生数为n,则m,n的值分别为( )
为了解某校身高在1.60m~1.78m的高一学生的情况,随机地抽查了该校100名高一学生,得到如图所示频率直方图.由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为m,身高在1.66m~1.74m的学生数为n,则m,n的值分别为( )| A、0.27,78 |
| B、0.27,83 |
| C、0.81,78 |
| D、0.09,83 |
如图所示将若干个点摆成三角形图案,每条边(色括两个端点)有n(n>l,n∈N*)个点,相应的图案中总的点数记为an,则
+
+
+…+
=( )

| 9 |
| a2a3 |
| 9 |
| a3a4 |
| 9 |
| a4a5 |
| 9 |
| a2013a2014 |

A、
| ||
B、
| ||
C、
| ||
D、
|
抛物线y2=4x,M(1,1)为其弦AB的中点,则AB方程为( )
| A、4x-2y-1=0 |
| B、4x-2y+1=0 |
| C、2x-y-1=0 |
| D、2x-y+1=0 |
在数列{an}中,已知a3=1,a5=3,a7=9,则{an}一定( )
| A、是等差数列 |
| B、是等比数列 |
| C、不是等差数列 |
| D、不是等比数列 |
甲乙两人通过考试的概率分别为
和
,两人同时参加考试,其中恰有一人通过的概率是( )
| 3 |
| 5 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
对于方程|x2-3x+2|=m(x-
)的实根个数,以下说法正确的是( )
| 3 |
| 2 |
| A、存在实数m,使得方程无解 |
| B、存在实数m,使得方程恰有1根 |
| C、无论m取任何实数,方程恰有2根 |
| D、无论m取任何实数,方程恰有4根 |
已知函数f(x)=cosx-
(x∈R,x≠0),则f′(1)值为( )
| 1 |
| x |
| A、-1-sin1 |
| B、1+sin1 |
| C、-1+sin1 |
| D、1-sin1 |