题目内容
已知函数f(x)=x+
(a>0).
(1)求f(x)的单调区间.
(2)判断函数f(x)在区间(0,4)上的单调性.
| a |
| x |
(1)求f(x)的单调区间.
(2)判断函数f(x)在区间(0,4)上的单调性.
考点:函数单调性的判断与证明,函数单调性的性质
专题:导数的综合应用
分析:(1)求f(x)的导数f′(x),利用导数判定函数f(x)的单调性和单调区间;
(2)结合(1),讨论a的取值,判定f(x)在区间(0,4)上的单调性.
(2)结合(1),讨论a的取值,判定f(x)在区间(0,4)上的单调性.
解答:
解:(1)∵f(x)=x+
(a>0),
∴f′(x)=1-
=
,
令f′(x)=0,解得x=±
;
∴当x<-
,或x>
时,f′(x)<0,f(x)是减函数;
当-
<x<
时,f′(x)>0,f(x)是增函数;
∴f(x)的减区间是(-∞,-
)和(
,+∞),增区间是(-
,
);
(2)当
≥4,即a≥16时,f′(x)在(0,4)上大于0,∴f(x)是增函数;
当
<4,即0<a<16时,在x∈(0,
)时,f′(x)>0,f(x)是增函数,
在x∈(
,4)时,f′(x)<0,f(x)是减函数.
综上,a≥16时,f(x)在(0,4)上是增函数;
0<a<16时,f(x)在(0,
)上是增函数,
在(
,4)上是减函数.
| a |
| x |
∴f′(x)=1-
| a |
| x2 |
| x2-a |
| x2 |
令f′(x)=0,解得x=±
| a |
∴当x<-
| a |
| a |
当-
| a |
| a |
∴f(x)的减区间是(-∞,-
| a |
| a |
| a |
| a |
(2)当
| a |
当
| a |
| a |
在x∈(
| a |
综上,a≥16时,f(x)在(0,4)上是增函数;
0<a<16时,f(x)在(0,
| a |
在(
| a |
点评:本题考查了利用函数的导数判定函数单调性问题,也考查了对字母系数的分类讨论问题,是中档题.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
抛物线y2=4x,M(1,1)为其弦AB的中点,则AB方程为( )
| A、4x-2y-1=0 |
| B、4x-2y+1=0 |
| C、2x-y-1=0 |
| D、2x-y+1=0 |
已知函数f(x)=cosx-
(x∈R,x≠0),则f′(1)值为( )
| 1 |
| x |
| A、-1-sin1 |
| B、1+sin1 |
| C、-1+sin1 |
| D、1-sin1 |
 如图,在平行四边形ABCD中,AB=2AD,∠BAD=60°,E为AB的中点,将△ADE沿直线DE折起到△PDE的位置,使平面PDE⊥平面BCDE.
如图,在平行四边形ABCD中,AB=2AD,∠BAD=60°,E为AB的中点,将△ADE沿直线DE折起到△PDE的位置,使平面PDE⊥平面BCDE.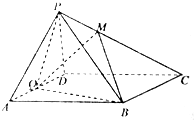 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,点Q为线段AD中点,PQ与QB不垂直.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,点Q为线段AD中点,PQ与QB不垂直. 如图,在四棱椎P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2的菱形,∠ABC=
如图,在四棱椎P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2的菱形,∠ABC=