题目内容
8.已知数列{an}各项都是正数,且$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+$\sqrt{{a}_{3}}$+…+$\sqrt{{a}_{n}}$=n2+3n(n∈N*).(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=$\frac{{a}_{n}}{(n+1)•{2}^{n}}$,n∈N*,求{bn}的前n项和Sn.
分析 (Ⅰ)当n≥2时利用$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+$\sqrt{{a}_{3}}$+…+$\sqrt{{a}_{n}}$=n2+3n与$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+$\sqrt{{a}_{3}}$+…+$\sqrt{{a}_{n-1}}$=(n-1)2+3(n-1)作差、整理可知an=4(n+1)2(n≥2),进而计算可得结论;
(Ⅱ)通过(I)可知bn=$\frac{4(n+1)}{{2}^{n}}$,n∈N*,进而利用错位相减法计算即得结论.
解答 解:(Ⅰ)当n≥2时,$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+$\sqrt{{a}_{3}}$+…+$\sqrt{{a}_{n}}$=n2+3n,
$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+$\sqrt{{a}_{3}}$+…+$\sqrt{{a}_{n-1}}$=(n-1)2+3(n-1),
两式相减得:$\sqrt{{a}_{n}}$=(n2+3n)-[(n-1)2+3(n-1)]=2n+2,
∴an=4(n+1)2(n≥2),
又∵$\sqrt{{a}_{1}}$=4即a1=16满足上式,
∴an=4(n+1)2;
(Ⅱ)由(I)可知bn=$\frac{{a}_{n}}{(n+1)•{2}^{n}}$=$\frac{4(n+1)}{{2}^{n}}$,n∈N*,
∴Sn=4[2•$\frac{1}{2}$+3•$\frac{1}{{2}^{2}}$+…+(n+1)•$\frac{1}{{2}^{n}}$],
$\frac{1}{2}$Sn=4[2•$\frac{1}{{2}^{2}}$+3•$\frac{1}{{2}^{3}}$+…+n•$\frac{1}{{2}^{n}}$+(n+1)•$\frac{1}{{2}^{n+1}}$],
两式相减得:$\frac{1}{2}$Sn=4[1+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$-(n+1)•$\frac{1}{{2}^{n+1}}$]
=4[1+$\frac{\frac{1}{{2}^{2}}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$-(n+1)•$\frac{1}{{2}^{n+1}}$]
=6-(n+3)•$\frac{1}{{2}^{n-1}}$,
于是Sn=12-(n+3)•$\frac{1}{{2}^{n-2}}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,考查错位相减法,注意解题方法的积累,属于中档题.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案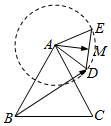 如图,等边△ABC的边长为2,△ADE也是等边三角形且边长为1,M为DE的中心,在△ABC所在平面内,△ADE绕A逆时针旋转一周,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为( )
如图,等边△ABC的边长为2,△ADE也是等边三角形且边长为1,M为DE的中心,在△ABC所在平面内,△ADE绕A逆时针旋转一周,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{4}$+$\sqrt{3}$ | C. | $\frac{3+\sqrt{3}}{4}$ | D. | $\frac{3}{4}$+2$\sqrt{3}$ |
| A. | {a|0≤a<1} | B. | {a|-1<a≤0} | C. | {a|-1<a<1} | D. | {a|a∈R,a∉Z} |
| A. | x+y-1=0 | B. | x-y+1=0 | C. | x+y+1=0 | D. | x-y-1=0 |