题目内容
18.函数$f(x)=2{sin^2}ωx+\sqrt{3}sin2ωx$(ω>0)的一条对称轴为直线$x=\frac{π}{8}$,则f(x)的最小正周期为$\frac{π}{4k+\frac{8}{3}}$,k∈Z,k≥0.分析 利用三角函数恒等变换的应用化简函数解析式可得f(x)=2sin(2ωx-$\frac{π}{6}$)+1,由2ωx-$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,解得函数f(x)的对称轴方程为:x=$\frac{kπ+\frac{2π}{3}}{2ω}$,k∈Z,由题意可得$\frac{π}{8}$=$\frac{kπ+\frac{2π}{3}}{2ω}$,k∈Z,解得ω,利用三角函数周期公式即可得解.
解答 解:∵$f(x)=2{sin^2}ωx+\sqrt{3}sin2ωx$
=1-cos2ωx+$\sqrt{3}$sin2ωx
=2($\frac{\sqrt{3}}{2}$sin2ωx-$\frac{1}{2}$cos2ωx)+1
=2sin(2ωx-$\frac{π}{6}$)+1,
∴由2ωx-$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,解得函数f(x)的对称轴方程为:x=$\frac{kπ+\frac{2π}{3}}{2ω}$,k∈Z,
∵函数f(x)的一条对称轴为直线$x=\frac{π}{8}$,
∴$\frac{π}{8}$=$\frac{kπ+\frac{2π}{3}}{2ω}$,k∈Z,解得:ω=4(k+$\frac{2}{3}$),k∈Z,k≥0,
∴f(x)的最小正周期T=$\frac{2π}{2ω}$=$\frac{2π}{8(k+\frac{2}{3})}$=$\frac{π}{4k+\frac{8}{3}}$,k∈Z,k≥0,
故答案为:$\frac{π}{4k+\frac{8}{3}}$,k∈Z,k≥0.
点评 本题主要考查了三角函数恒等变换的应用,三角函数周期公式,正弦函数的图象和性质,考查了计算能力和数形结合思想,属于中档题.

 名校课堂系列答案
名校课堂系列答案(Ⅰ)求抛物线C的准线方程;
(Ⅱ)求实数k的取值范围;
(Ⅲ)若线段AB中点的横坐标为2,求AB的长度.
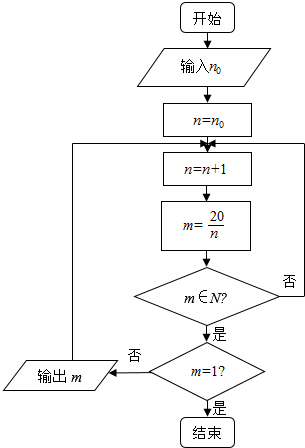 阅读如图程序框图,其中n0∈N.若输出的结果中,只有三个自然数,则输入的自然数n0的所有可能的值为( )
阅读如图程序框图,其中n0∈N.若输出的结果中,只有三个自然数,则输入的自然数n0的所有可能的值为( )| A. | 2,3,4 | B. | 2 | C. | 2,3 | D. | 3,4 |