题目内容
3.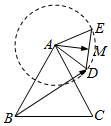 如图,等边△ABC的边长为2,△ADE也是等边三角形且边长为1,M为DE的中心,在△ABC所在平面内,△ADE绕A逆时针旋转一周,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为( )
如图,等边△ABC的边长为2,△ADE也是等边三角形且边长为1,M为DE的中心,在△ABC所在平面内,△ADE绕A逆时针旋转一周,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{4}$+$\sqrt{3}$ | C. | $\frac{3+\sqrt{3}}{4}$ | D. | $\frac{3}{4}$+2$\sqrt{3}$ |
分析 设∠BAD=θ,(0≤θ≤2π),则∠CAE=θ,把$\overrightarrow{BD}$•$\overrightarrow{AM}$转化为含有θ的三角函数,利用辅助角公式化积后得答案.
解答 解:设∠BAD=θ,(0≤θ≤2π),则∠CAE=θ,
则$\overrightarrow{BD}$•$\overrightarrow{AM}$=($\overrightarrow{AD}-\overrightarrow{AB}$)•$\frac{1}{2}$($\overrightarrow{AD}+\overrightarrow{AE}$)=$\frac{1}{2}({\overrightarrow{AD}}^{2}+\overrightarrow{AD}•\overrightarrow{AE}-\overrightarrow{AB}•\overrightarrow{AD}-\overrightarrow{AB}•\overrightarrow{AE})$
=$\frac{1}{2}$$+\frac{1}{4}$$-\frac{1}{2}×2×1×cos(θ+\frac{π}{3})$
=$\frac{3}{4}$-cosθ-cosθcos$\frac{π}{3}$+sinθsin$\frac{π}{3}$
=$\frac{3}{4}$-$\frac{3}{2}cosθ+\frac{\sqrt{3}}{2}sinθ$
=$\sqrt{3}sin(θ-\frac{π}{6})+\frac{3}{4}$.
∴当$θ=\frac{2π}{3}$时,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为$\sqrt{3}+\frac{3}{4}$.
故选:B.
点评 本题考查平面向量的数量积的定义,考查三角函数的化简和求最值,考查运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案(Ⅰ)求抛物线C的准线方程;
(Ⅱ)求实数k的取值范围;
(Ⅲ)若线段AB中点的横坐标为2,求AB的长度.
| A. | 点(π,0)是函数y=f(x)图象的一个对称中心 | |
| B. | 直线x=$\frac{π}{2}$是函数y=f(x)图象的一条对称轴 | |
| C. | π是函数y=f(x)的周期 | |
| D. | 函数y=f(x)的最大值为1 |
| 投入资金 | 甲产品利润 | 乙产品利润 |
| 4 | 1 | 2.5 |
| A. | $\frac{9}{2}$ | B. | $\frac{65}{16}$ | C. | $\frac{35}{8}$ | D. | $\frac{17}{4}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也必要条件 |