题目内容
18.命题“?x<0,使得方程2x+a=$\frac{1}{x-1}$有解”是真命题,则实数a的取值范围是(-2,0).分析 当 x∈(-∞,0)时,函数y=2x与y=$\frac{1}{x-1}$分别是单调递增与单调递减函数,可得函数f(x)=2x-$\frac{1}{x-1}$单调性,求其在x<0时的范围,进而得出a的取值范围.
解答 解:当 x∈(-∞,0)时,函数y=2x与y=$\frac{1}{x-1}$分别是单调递增与单调递减函数.
∴函数f(x)=2x-$\frac{1}{x-1}$单调递增.
∴f(x)<f(0)=20+1=2.
又当x→-∞时,f(x)→0,
∴0<f(x)<2.
∵?x<0,使得方程2x+a=$\frac{1}{x-1}$有解,
∴-a∈(0,2),即a∈(-2,0).
故答案为:(-2,0).
点评 本题考查了函数的单调性和存在性问题的解法,考查数学转化思想方法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知全集为R,A=[1,+∞),B=(0,+∞),则(∁RA)∩B等于( )
| A. | (-∞,0) | B. | (0,1) | C. | (0,1] | D. | (1,+∞) |
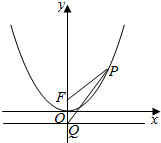 如图,设抛物线x2=4y的焦点为F,其准线与y轴相交于点Q,设P为抛物线上的一点,若$|{PQ}|=\sqrt{2}|{PF}|$,则△PQF的面积为2.
如图,设抛物线x2=4y的焦点为F,其准线与y轴相交于点Q,设P为抛物线上的一点,若$|{PQ}|=\sqrt{2}|{PF}|$,则△PQF的面积为2.