题目内容
17．直线l：x-y+1=0关于x轴对称的直线方程为（ ）| A． | x+y-1=0 | B． | x-y+1=0 | C． | x+y+1=0 | D． | x-y-1=0 |
分析 直线l：x-y+1=0即y=x+1关于x轴对称的直线方程为的斜率为-1，在y轴上的截距为-1，即可得出．
解答 解：直线l：x-y+1=0即y=x+1关于x轴对称的直线方程为的斜率为-1，在y轴上的截距为-1，
∴要求的直线方程为：y=-x-1，即x+y+1=0．
故选：C．
点评 本题考查了直线的对称性、直线方程，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
5．已知函数f（x）=cosx+ax2-1，a∈R，若对于任意的实数x恒有f（x）≥0，则实数a的取值范围是（ ）
| A． | [$\frac{1}{2}$，+∞） | B． | （$\frac{1}{2}$，+∞） | C． | [-$\frac{1}{4}$，+∞） | D． | （$\frac{1}{4}$，+∞） |
2．若f（x）在x0处连接，则下列命题中正确的是（ ）
| A． | 若f（x0）是f（x）的极值，则f（x）在x0处可导且f′（x0）=0 | |
| B． | 若曲线y=f（x）在x0附近的左侧切线斜率为正，右侧切线斜率为负，则f（x0）是f（x）的极大值 | |
| C． | 若曲线y=f（x）在x0附近的左侧切线斜率为负，右侧切线斜率为正，则f（x0）是f（x）的极大值 | |
| D． | 若f′（x0）=0，则f（x0）必是f（x）的极值 |
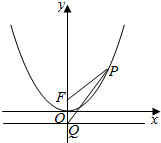如图，设抛物线x2=4y的焦点为F，其准线与y轴相交于点Q，设P为抛物线上的一点，若$|{PQ}|=\sqrt{2}|{PF}|$，则△PQF的面积为2．