题目内容
20．方程[x]=x+a有解（[x]表示不大于x的最大整数），则参数a的取值集合是（ ）| A． | {a|0≤a＜1} | B． | {a|-1＜a≤0} | C． | {a|-1＜a＜1} | D． | {a|a∈R，a∉Z} |
分析 化简a=[x]-x，从而确定-1＜[x]-x≤0，从而解得．
解答 解：∵[x]=x+a，
∴a=[x]-x，
∵[x]表示不大于x的最大整数，
∴-1＜[x]-x≤0，
∴参数a的取值集合是{a|-1＜a≤0}，
故选B．
点评 本题考查了方程的根与函数的零点的关系应用及学生的化简运算能力．
练习册系列答案
相关题目
10．
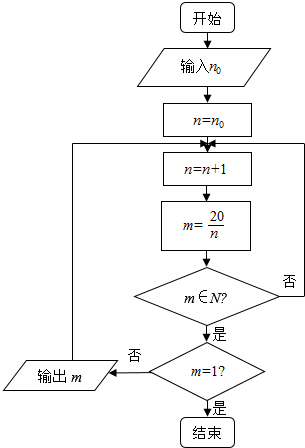阅读如图程序框图，其中n0∈N．若输出的结果中，只有三个自然数，则输入的自然数n0的所有可能的值为（ ）
阅读如图程序框图，其中n0∈N．若输出的结果中，只有三个自然数，则输入的自然数n0的所有可能的值为（ ）| A． | 2，3，4 | B． | 2 | C． | 2，3 | D． | 3，4 |
11．设函数f（x）=sinxcos2x，则下列结论中错误的为（ ）
| A． | 点（π，0）是函数y=f（x）图象的一个对称中心 | |
| B． | 直线x=$\frac{π}{2}$是函数y=f（x）图象的一条对称轴 | |
| C． | π是函数y=f（x）的周期 | |
| D． | 函数y=f（x）的最大值为1 |
15．在△ABC中，内角A，B，C的对边分别为a，b，c，则“cosA=$\frac{b}{c}$”是“△ABC为Rt△”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也必要条件 |
5．已知函数f（x）=cosx+ax2-1，a∈R，若对于任意的实数x恒有f（x）≥0，则实数a的取值范围是（ ）
| A． | [$\frac{1}{2}$，+∞） | B． | （$\frac{1}{2}$，+∞） | C． | [-$\frac{1}{4}$，+∞） | D． | （$\frac{1}{4}$，+∞） |