题目内容
19.一种放射性元素,最初的质量为1000克,按每年10%衰减.(1)试写出t(t∈N*)年后,这种放射性元素的质量y与t的函数关系式;
(2)求这种放射性元素的半衰期(质量变为原来的$\frac{1}{2}$时所经历的时间).(lg2≈0.3,lg3≈0.47).
分析 (1)最初的质量为1000g,经过1年,y=1000(1-10%)=1000×0.9,经过2年,y=1000(1-10%)2=1000×0.92,由此规律可得;
(2)由题意可得方程1000×0.9t=500,两边取常用对数,代入近似值计算可得.
解答 解:(1)最初的质量为1000g,
经过1年,y=1000(1-10%)=1000×0.9,
经过2年,y=1000(1-10%)2=1000×0.92
经过t年,y=1000(1-10%)t=1000×0.9t
(2)解方程1000×0.9t=500,
两边取常用对数tlg0.9=lg0.5,
解得t=$\frac{-lg2}{2lg3-1}$≈$\frac{0.3}{1-2×0.47}$=5
即这种放射性元素的半衰期约为5年.
点评 本题考查等比数列的通项公式,从实际问题得出规律是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.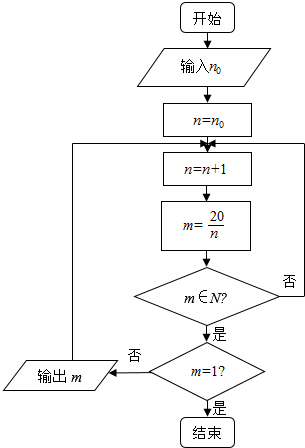 阅读如图程序框图,其中n0∈N.若输出的结果中,只有三个自然数,则输入的自然数n0的所有可能的值为( )
阅读如图程序框图,其中n0∈N.若输出的结果中,只有三个自然数,则输入的自然数n0的所有可能的值为( )
 阅读如图程序框图,其中n0∈N.若输出的结果中,只有三个自然数,则输入的自然数n0的所有可能的值为( )
阅读如图程序框图,其中n0∈N.若输出的结果中,只有三个自然数,则输入的自然数n0的所有可能的值为( )| A. | 2,3,4 | B. | 2 | C. | 2,3 | D. | 3,4 |
11.设函数f(x)=sinxcos2x,则下列结论中错误的为( )
| A. | 点(π,0)是函数y=f(x)图象的一个对称中心 | |
| B. | 直线x=$\frac{π}{2}$是函数y=f(x)图象的一条对称轴 | |
| C. | π是函数y=f(x)的周期 | |
| D. | 函数y=f(x)的最大值为1 |