题目内容
过椭圆
+
=1的焦点F1，F2分别作互相垂直的直线l1，l2，
（1）直线l1，l2交于P（x0，y0），求证：
+
＜1
（2）若直线l1，l2分别与椭圆交于A，C和B，D，
（i）求证：
+
=定值
（ii）求四边形ABCD面积的最小值．
| x2 |
| 3 |
| y2 |
| 2 |
（1）直线l1，l2交于P（x0，y0），求证：
| x02 |
| 3 |
| y02 |
| 2 |
（2）若直线l1，l2分别与椭圆交于A，C和B，D，
（i）求证：
| 1 |
| |AC| |
| 1 |
| |BD| |
（ii）求四边形ABCD面积的最小值．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）由已知条件得
•
=0，所以x02+y02=1，由此能证明
+
＜1．
（2）（i）证明：设l1：y=k（x+1），l2：y=-
(x-1)，由
，得（2+3k2）x2+6k2x+3k2-6=0，|AC|=
，同理：|BD|=
，由此能证明
+
=
．
（ii）由
+
=
≥
，得|AC|•|BD|≥
，由此能求出四边形ABCD面积的最小值．
| PF1 |
| PF2 |
| x02 |
| 3 |
| y02 |
| 2 |
（2）（i）证明：设l1：y=k（x+1），l2：y=-
| 1 |
| k |
|
4
| ||
| 2+3k2 |
4
| ||
| 3+2k2 |
| 1 |
| |AC| |
| 1 |
| |BD| |
5
| ||
| 12 |
（ii）由
| 1 |
| |AC| |
| 1 |
| |BD| |
5
| ||
| 12 |
| 2 | ||
|
| 192 |
| 25 |
解答：
（1）解：由
+
=1的焦点F1（-1，0），F2（1，0），
∵过椭圆
+
=1的焦点F1，F2分别作互相垂直的直线l1，l2，
∴
•
=0，
∴x02+y02=1，（1分）
∴
+
＜x02+y02=1．（2分）
（2）（i）证明：设l1：y=k（x+1），l2：y=-
(x-1)，
，
（2+3k2）x2+6k2x+3k2-6=0，（3分）
|AC|=
=
，（4分）
同理：|BD|=
．（5分）
∴
+
=
=
．（7分）
（ii）∵
+
=
≥
，
∴|AC|•|BD|≥
，
∴SABCD=
|AC|•|BD|≥
，
∴四边形ABCD面积的最小值是
．
| x2 |
| 3 |
| y2 |
| 2 |
∵过椭圆
| x2 |
| 3 |
| y2 |
| 2 |
∴
| PF1 |
| PF2 |
∴x02+y02=1，（1分）
∴
| x02 |
| 3 |
| y02 |
| 2 |
（2）（i）证明：设l1：y=k（x+1），l2：y=-
| 1 |
| k |
|
（2+3k2）x2+6k2x+3k2-6=0，（3分）
|AC|=
| ||||
| 2+3k2 |
4
| ||
| 2+3k2 |
同理：|BD|=
4
| ||
| 3+2k2 |
∴
| 1 |
| |AC| |
| 1 |
| |BD| |
| 2+3k2+3+2k2 | ||
4
|
5
| ||
| 12 |
（ii）∵
| 1 |
| |AC| |
| 1 |
| |BD| |
5
| ||
| 12 |
| 2 | ||
|
∴|AC|•|BD|≥
| 192 |
| 25 |
∴SABCD=
| 1 |
| 2 |
| 96 |
| 25 |
∴四边形ABCD面积的最小值是
| 96 |
| 25 |
点评：本题考查不等式的证明，考查两数和为定值的证明，考查四边形面积的最小值的求法，解题时要认真审题，注意两点间距离公式的合理运用．
练习册系列答案
相关题目
如图所示，等边△ABC的边长为2，以A为圆心，半径为1作圆，PQ是圆的直径，求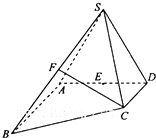
如图，在四棱锥S-ABCD中，己如AB∥DC，AB⊥AD，△SAD是正三角形，AD=AB=2DC=2，SC=
在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，M，N分别是AB，PC的中点．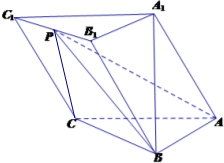
如图，在三棱柱ABC-A1B1C1中，AB⊥AC，顶点A1在底面ABC上的射影恰为点B，且AB=AC=A1B=2．