题目内容
函数f（x）=
+lg
的定义域是（ ）
| ||
| x-3 |
| 4-x |
| A、（2，4） |
| B、（3，4） |
| C、（2，3）∪（3，4] |
| D、[2，3）∪（3，4） |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件，即可求函数的定义域．
解答：
解：要使函数有意义，则
，
即
，
解得：2≤x＜3或3＜x＜4，
故函数的定义域为[2，3）∪（3，4）．
故选：D．
|
即
|
解得：2≤x＜3或3＜x＜4，
故函数的定义域为[2，3）∪（3，4）．
故选：D．
点评：本题主要考查函数定义域的求法，根据函数成立的条件是解决此类问题的关键．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
| 10 |
| 3 |
| 14 |
| 7 |
| A、＞ | B、≥ | C、≤ | D、＜ |
（理科）曲线y=sinx，x∈[0，2π]与直线y=0围成的两个封闭区域面积之和为（ ）
| A、0 | B、1 | C、2 | D、4 |
下列不等式可以推出a＞b的是（ ）
| A、ac＞bc | ||||
B、
| ||||
| C、a+c＞b+d | ||||
| D、a-c＞b-c |
函数y=Acos（ωx+φ）+b（A＞0）的最大值为5，最小值为1，则A=（ ）
| A、1 | B、2 | C、3 | D、4 |
设函数f（x）=|lnx|，则下列结论中正确的是（ ）
A、f（1）＜f（
| ||
B、f（
| ||
C、f（e）＜f（1）＜f（
| ||
D、f（e）＜f（
|
设ab＞0，下面四个不等式中，正确的是（ ）
①|a+b|＞|a|；②|a+b|＜|b|；③|a+b|＜|a-b|；④|a+b|＞|a|-|b|
①|a+b|＞|a|；②|a+b|＜|b|；③|a+b|＜|a-b|；④|a+b|＞|a|-|b|
| A、①和② | B、①和③ |
| C、①和④ | D、②和④ |
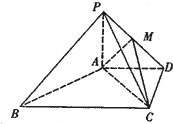如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，PB⊥AC，AD⊥CD，且AD=CD=2