题目内容
以下命题：
①若|
•
|=|
|•|
|，则
∥
；
②
=（-1，1）在
=（3，4）方向上的投影为
；
③若△ABC中，a=5，b=8，c=7，则
•
=20；
④若非零向量
、
满足|
+
|=|
|，则|2
|＞|
+2
|．
所有真命题的标号是 ．
①若|
| a |
| b |
| a |
| b |
| a |
| b |
②
| a |
| b |
| 1 |
| 5 |
③若△ABC中，a=5，b=8，c=7，则
| BC |
| CA |
④若非零向量
| a |
| b |
| a |
| b |
| b |
| b |
| a |
| b |
所有真命题的标号是
考点：命题的真假判断与应用,向量的模,平面向量数量积的运算
专题：综合题,平面向量及应用
分析：①由|
•
|=|
|•|
|得出两向量的夹角为0°或180°，判断命题正确；
②求出
在
方向上的投影即可；
③画出图形，结合图形求出
•
的值即可；
④由|
+
|=|
|，得出2
•
=-
2，由4
2＞(
+2
)2，即得|2
|＞|
+2
|．
| a |
| b |
| a |
| b |
②求出
| a |
| b |
③画出图形，结合图形求出
| BC |
| CA |
④由|
| a |
| b |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
解答：
解：对于①，当|
•
|=|
|•|
|时，cos＜
，
＞=±1，两向量的夹角为0°或180°，
∴
∥
，命题正确；
对于②，
=（-1，1）在
=（3，4）方向上的投影是
|
|cos＜
，
＞=
=
=
，∴命题正确；
对于③，△ABC中，如图所示；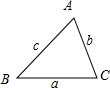
a=5，b=8，c=7，
∴cos＜
，
＞=-
=-
=-
，
•
=5×8×（-
）=-20，∴命题错误；
对于④，∵非零向量
、
满足|
+
|=|
|，∴
2+2
•
=0，
即2
•
=-
2；
∴4
2-(
+2
)2=-
2-4
•
=-
2-（-2
2）=
2＞0，
∴4
2＞(
+2
)2；
即|2
|＞|
+2
|，∴命题正确．
综上，正确的命题是①②④．
故答案为：①②④．
| a |
| b |
| a |
| b |
| a |
| b |
∴
| a |
| b |
对于②，
| a |
| b |
|
| a |
| a |
| b |
| ||||
|
|
| -1×3+1×4 | ||
|
| 1 |
| 5 |
对于③，△ABC中，如图所示；
a=5，b=8，c=7，
∴cos＜
| BC |
| CA |
| a2+b2-c2 |
| 2ab |
| 25+64-49 |
| 2×5×8 |
| 1 |
| 2 |
| BC |
| CA |
| 1 |
| 2 |
对于④，∵非零向量
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
即2
| a |
| b |
| a |
∴4
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| a |
| a |
∴4
| b |
| a |
| b |
即|2
| b |
| a |
| b |
综上，正确的命题是①②④．
故答案为：①②④．
点评：本题考查了平面向量的应用问题，也考查了命题真假的判断问题，解题时应对每一个选项进行分析判断，从而得出正确的结论．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
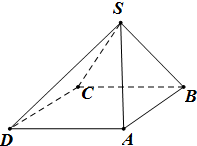四棱锥S-ABCD中，底面ABCD为平行四边形，侧面SBC⊥底面ABCD，已知∠ABC=45°，AB=2，BC=2数列{an}的前n项和为n2，那么当n≥2时，{an}的通项公式为（ ）
| A、an=2n-1 | ||
| B、an=n2 | ||
C、an=
| ||
D、an=
|