题目内容
在数列{an}中,a1=1,an-2an+1+an+2=0(n∈N*),且a1,a2,a5成公比不等于1的等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
,数列{bn}的前n项和为Sn,求满足Sn>
的最小正整数n的值.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
| 1 |
| a2n-1+1 |
| 510 |
| 511 |
考点:等差数列的通项公式,等差关系的确定,等比关系的确定
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件得{an}成等差数列,设公差为d,则(1+d)2=1+4d,由此能求出an=2n-1.
(Ⅱ)由已知条件推导出bn=
,从而得到Sn=1-
,由此能求出满足Sn>
的最小正整数n的值.
(Ⅱ)由已知条件推导出bn=
| 1 |
| 2n |
| 1 |
| 2n |
| 510 |
| 511 |
解答:
满分(14分).
解:(Ⅰ)∵2an+1=an+an+2,
∴{an}成等差数列,
设公差为d,则(1+d)2=1+4d,解得d=2(d=0舍去)
∴an=2n-1.(7分)
(Ⅱ)∵an=2n-1,
∴bn=
=
=
,(9分)
∴Sn=1-
,(11分)
∴Sn>
=1-
,
即2n>511(n∈N*),
∴nmin=9,
∴满足Sn>
的最小正整数n的值是9.(14分)
解:(Ⅰ)∵2an+1=an+an+2,
∴{an}成等差数列,
设公差为d,则(1+d)2=1+4d,解得d=2(d=0舍去)
∴an=2n-1.(7分)
(Ⅱ)∵an=2n-1,
∴bn=
| 1 |
| a2n-1+1 |
| 1 |
| 2•2n-1+1-1 |
| 1 |
| 2n |
∴Sn=1-
| 1 |
| 2n |
∴Sn>
| 510 |
| 511 |
| 1 |
| 511 |
即2n>511(n∈N*),
∴nmin=9,
∴满足Sn>
| 510 |
| 511 |
点评:本题主要考查等差数列、等比数列的概念,等差数列的通项公式、求和公式等基础知识,同时考查运算求解能力.

练习册系列答案
相关题目
已知i为虚数单位,a为实数,复数z=(a-2i)•i在复平面内对应的点为M,则“a=-1”是“点M在第四象限”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知角θ的顶点与原点重合,始边与x轴的非负半轴重合,终边在直线y=2x上,则sin2θ等于( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
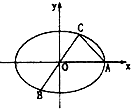 如图,已知椭圆
如图,已知椭圆 已知直线l:y=kx+2(k为常数)过椭圆C:
已知直线l:y=kx+2(k为常数)过椭圆C: