题目内容
在△ABC中,内角A,B,C所对边分别为a,b,c,且
=
.
(1)求角B的大小;
(2)如果b=2,求△ABC面积的最大值.
| sinA |
| a |
| ||
| b |
(1)求角B的大小;
(2)如果b=2,求△ABC面积的最大值.
考点:余弦定理,正弦定理
专题:三角函数的求值,解三角形
分析:(1)已知等式利用正弦定理化简,求出tanB的值,即可确定出B的度数;
(2)利用余弦定理表示出cosB,将b与cosB的值代入,整理得到关系式,利用基本不等式化简求出ac的最大值,再由sinB的值,利用三角形面积公式即可求出三角形ABC面积的最大值.
(2)利用余弦定理表示出cosB,将b与cosB的值代入,整理得到关系式,利用基本不等式化简求出ac的最大值,再由sinB的值,利用三角形面积公式即可求出三角形ABC面积的最大值.
解答:
解:(1)已知等式
=
,由正弦定理得
=
,即tanB=
,
∴B=
;
(2)∵b=2,cosB=
,
∴cosB=
=
,
∴a2+c2=ac+4,
又∴a2+c2≥2ac,
∴ac≤4,当且仅当a=c取等号,
∴S=
acsinB≤
,
则△ABC为正三角形时,Smax=
.
| sinA |
| a |
| ||
| b |
| sinA |
| sinA |
| ||
| sinB |
| 3 |
∴B=
| π |
| 3 |
(2)∵b=2,cosB=
| 1 |
| 2 |
∴cosB=
| a2+b2-4 |
| 2ac |
| 1 |
| 2 |
∴a2+c2=ac+4,
又∴a2+c2≥2ac,
∴ac≤4,当且仅当a=c取等号,
∴S=
| 1 |
| 2 |
| 3 |
则△ABC为正三角形时,Smax=
| 3 |
点评:此题考查了正弦、余弦定理,以及三角形面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
已知向量
=(-1,1),
=(3,m),若
⊥
,则实数m=( )
| a |
| b |
| a |
| b |
| A、1 | B、-1 | C、3 | D、-3 |
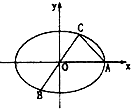 如图,已知椭圆
如图,已知椭圆 已知直线l:y=kx+2(k为常数)过椭圆C:
已知直线l:y=kx+2(k为常数)过椭圆C: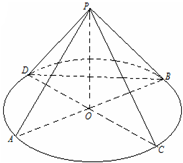 如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC
如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为平行四边形,AD=A1A=
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为平行四边形,AD=A1A=