题目内容
2．下列参数方程（t为参数）与普通方程x2-y=0表示同一曲线的方程是（ ）| A． | $\left\{\begin{array}{l}x=tant\\ y=\frac{1+cos2t}{1-cos2t}\end{array}$ | B． | $\left\{\begin{array}{l}x=tant\\ y=\frac{1-cos2t}{1+cos2t}\end{array}$ | ||
| C． | $\left\{\begin{array}{l}{x=|t|}\\{y={t}^{2}}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=cost}\\{y=co{s}_{\;}^{2}t}\end{array}\right.$． |
分析 根据x，y的范围及对应关系进行判断．
解答 解：∵x2-y=0，∴x∈R，y≥0．排除C，D．
若x=tant，则y=tan2t=$\frac{si{n}^{2}t}{co{s}^{2}t}$=$\frac{1-cos2t}{1+cos2t}$．排除A．
故选：B．
点评 本题考查了曲线的参数方程，注意x，y的取值范围是解题关键，属于基础题．
练习册系列答案
相关题目
12．已知cosα=$\frac{\sqrt{5}}{7}$，且sinα＜0，则角α是（ ）
| A． | 第一象限角 | B． | 第二象限角 | C． | 第三象限角 | D． | 第四象限角 |
13．已知A（0，1），B（-3，4），若∠AOB的平分线交AB于D点，则$\overrightarrow{AD}$=（ ）
| A． | （$\frac{1}{2}$，$\frac{1}{2}$） | B． | （-$\frac{1}{2}$，$\frac{1}{2}$） | C． | （$\frac{1}{2}$，-$\frac{1}{2}$） | D． | （-$\frac{1}{2}$，-$\frac{1}{2}$） |
17．函数y=1-cos2x的定义域是（ ）
| A． | （-∞，0] | B． | [0，+∞） | C． | [-1，1] | D． | （-∞，+∞） |
14．已知α的终边和单位圆的交点坐标是（$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$），则sin（$\frac{π}{2}$-α）cos（π+α）的值是（ ）
| A． | $\frac{\sqrt{3}}{4}$ | B． | -$\frac{\sqrt{3}}{4}$ | C． | -$\frac{3}{4}$ | D． | $\frac{3}{4}$ |
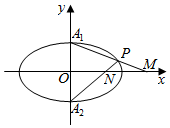已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个焦点为F1（-$\sqrt{3}$，0），且过点E（$\sqrt{3}$，$\frac{1}{2}$），设椭圆C的上下顶点分别为A1，A2，点P是椭圆上异于A1，A2的任一点，直线PA1，PA2分别交x轴于点M，N．