题目内容
下列命题中,错误的是( )
| A、平行于同一平面的两个不同平面平行 |
| B、一条直线与两个平行平面中的一个相交,则必与另一个平面相交 |
| C、若直线l与平面α相交但不垂直,则经过该直线l有且只有一个平面β与α垂直 |
| D、若直线l不平行平面α,则在平面α内不存在与l平行的直线 |
考点:空间中直线与平面之间的位置关系,平面与平面之间的位置关系
专题:空间位置关系与距离
分析:根据空间直线和平面垂直和平行的性质和判定定理分别进行判定即可得到结论.
解答:
解:A.根据面面平行的性质可知,平行于同一平面的两个不同平面平行,正确.
B.若一条直线与两个平行平面中的一个相交,则必与另一个平面相交,正确.
C.直线l与平面α相交但不垂直,则经过该直线l有且只有一个平面β与α垂直,正确.
D.当直线l?α,满足直线l不平行平面α,此时平面α内存在无数条直线和l平行,故D错误.
故选:D
B.若一条直线与两个平行平面中的一个相交,则必与另一个平面相交,正确.
C.直线l与平面α相交但不垂直,则经过该直线l有且只有一个平面β与α垂直,正确.
D.当直线l?α,满足直线l不平行平面α,此时平面α内存在无数条直线和l平行,故D错误.
故选:D
点评:本题主要考查空间直线和平面位置关系的判定,要求熟练掌握平行和判定的判定定理.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
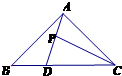 如图,在直角△ABC中,|
如图,在直角△ABC中,|| AB |
| AC |
| DC |
| BD |
| AP |
| CP |
A、[0,
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
若log0.5x>1,则x的取值范围是( )
A、(-∞,
| ||
B、(
| ||
C、(
| ||
D、(0,
|
已知a,b,c为△ABC的三边,若b2+c2-a2=bc,则
的取值范围是( )
| b+c |
| a |
| A、(1,2] | ||
B、(1,
| ||
C、[
| ||
D、(
|
执行如图所示的程序框图,则输出的结果是( )


| A、128 | B、127 |
| C、64 | D、63 |