题目内容
已知实数x,y满足条件
,若目标函数z=
+
(a>0,b>0)的最大值为9,则4a+b的最小值为( )
|
| x |
| a |
| y |
| b |
A、
| ||
| B、16 | ||
| C、4 | ||
D、
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用数形结合确定目标函数的最优解,利用基本不等式即可得到结论.
解答:
解:作出不等式组对应的平面区域如图:
由z=
+
(a>0,b>0)得y=-
x+bz,
∵a>0,b>0,∴y=-
x+bz的斜率k=-
<0,
平移直线y=-
x+bz,由图象可知当直线y=-
x+bz经过点B时,直线y=-
x+bz的截距最大,此时z最大,
由
,解得
,即B(1,4),
此时
+
=9,即
+
=1,
则4a+b=(4a+b)(
+
)=
+
+
+
≥
+2
=
+
=
,
当且仅当
=
,即b=4a时,取等号,
故选:A.

由z=
| x |
| a |
| y |
| b |
| a |
| b |
∵a>0,b>0,∴y=-
| a |
| b |
| a |
| b |
平移直线y=-
| a |
| b |
| a |
| b |
| a |
| b |
由
|
|
此时
| 1 |
| a |
| 4 |
| b |
| 1 |
| 9a |
| 4 |
| 9b |
则4a+b=(4a+b)(
| 1 |
| 9a |
| 4 |
| 9b |
| 4 |
| 9 |
| 4 |
| 9 |
| b |
| 9a |
| 16a |
| 9b |
| 8 |
| 9 |
|
| 8 |
| 9 |
| 8 |
| 9 |
| 16 |
| 9 |
当且仅当
| b |
| 9a |
| 16a |
| 9b |
故选:A.
点评:本题主要考查线性规划和基本不等式的应用,利用数形结合是解决本题的关键,综合性较强.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
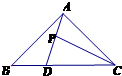 如图,在直角△ABC中,|
如图,在直角△ABC中,|| AB |
| AC |
| DC |
| BD |
| AP |
| CP |
A、[0,
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
执行如图所示的程序框图,则输出的结果是( )


| A、128 | B、127 |
| C、64 | D、63 |
在平面直角坐标系中,记由点A(0,1),B(4,2),C(2,6)围成的三角形区域(含边界)为D,P(x,y)为区域D上的点,则
最大值与最小值的和为( )
| (x-2)2+(y-2)2 |
A、
| ||||||||
B、
| ||||||||
| C、4 | ||||||||
D、
|
已知等比数列{an}的前n项和为Sn,且满足
=9,则公比q=( )
| S6 |
| S3 |
A、
| ||
B、±
| ||
| C、2 | ||
| D、±2 |
 如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD.AB=AD=
如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD.AB=AD=