题目内容
已知正四棱锥的侧棱与底面的边长都为3
，则这个四棱锥的外接球的表面积为 ．
| 2 |
考点：球的体积和表面积
专题：空间位置关系与距离
分析：先画出图形，正四棱锥外接球的球心在它的底面的中心，然后根据勾股定理解出球的半径，最后根据球的表面积公式解之即可．
解答：
解：如图，设正四棱锥底面的中心为O，则
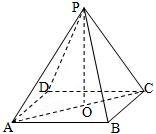
在直角三角形ABC中，AC=
×AB=6，
∴AO=CO=3，
在直角三角形PAO中，PO=
=
=3，
∴正四棱锥的各个顶点到它的底面的中心的距离都为3，
∴正四棱锥外接球的球心在它的底面的中心，且球半径r=3，
球的表面积S=4πr2=36π
故答案为：36π
在直角三角形ABC中，AC=
| 2 |
∴AO=CO=3，
在直角三角形PAO中，PO=
| PA2-AO2 |
(3
|
∴正四棱锥的各个顶点到它的底面的中心的距离都为3，
∴正四棱锥外接球的球心在它的底面的中心，且球半径r=3，
球的表面积S=4πr2=36π
故答案为：36π
点评：本题主要考查球的表面积，球的内接体问题，考查计算能力和空间想象能力，属于中档题．
练习册系列答案
黄冈小状元解决问题天天练系列答案
相关题目
等差数列中，如果a4+a6=22，则前9项的和为（ ）
| A、297 | B、144 |
| C、99 | D、66 |
下列函数中，与函数y=
定义域相同的函数为（ ）
| 1 | ||
|
A、y=
| ||
B、y=
| ||
| C、y=x-2 | ||
| D、y=lnx |
以双曲线y2-x2=2的一个焦点为圆心，离心率为半径的圆的方程是（ ）
| A、x2+（y±2）2=2 |
| B、（x±2）2+y2=2 |
| C、x2+（y±2）2=4 |
| D、（x±2）2+y2=4 |
一艘海轮从A处出发，以每小时60海里的速度沿东偏南50°方向直线航行，30分钟后到达B处，在C处有一座灯塔，海轮在A处观察灯塔，其方向是东偏南20°，在B处观察灯塔，其方向是北偏东65°，那么B、C两点间的距离是（ ）
A、10
| ||
B、10
| ||
C、15
| ||
D、20
|