题目内容
7.已知正数x,y满足约束条件$\left\{\begin{array}{l}{2x-y≤0}\\{x-3y+5≥0}\end{array}\right.$,则$z={(\frac{1}{2})^{2x+y}}$的最小值为$\frac{1}{16}$.分析 由约束条件作出可行域,令t=2x+y,化为y=-2x+t,数形结合求得t的最大值,进一步求得$z={(\frac{1}{2})^{2x+y}}$的最小值.
解答 解:由约束条件$\left\{\begin{array}{l}{x>0,y>0}\\{2x-y≤0}\\{x-3y+5≥0}\end{array}\right.$作出可行域如图,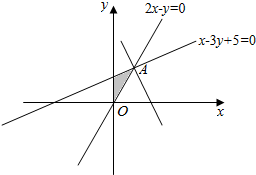
联立$\left\{\begin{array}{l}{2x-y=0}\\{x-3y+5=0}\end{array}\right.$,解得A(1,2).
令t=2x+y,化为y=-2x+t,
由图可知,当直线y=-2x+t过A时,t有最大值为4.
∴$z={(\frac{1}{2})^{2x+y}}$的最小值为$\frac{1}{16}$.
故答案为:$\frac{1}{16}$.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
18.已知向量$\overrightarrow p=(2,-3)$,$\overrightarrow q=(x,6)$,且$\overrightarrow p$∥$\overrightarrow q$,则$|{\overrightarrow p+\overrightarrow q}|$的值为( )
| A. | 13 | B. | 14 | C. | $\sqrt{13}$ | D. | $\sqrt{14}$ |
2.下列函数中,既是奇函数又存在零点的是( )
| A. | $f(x)=\sqrt{x}$ | B. | $f(x)=\frac{1}{x}$ | C. | f(x)=ex | D. | f(x)=sinx |
12.如图,A,B,C,D是平面上的任意四点,下列式子中正确的是( )
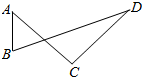

| A. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{BC}$+$\overrightarrow{DA}$ | B. | $\overrightarrow{AC}$+$\overrightarrow{BD}$=$\overrightarrow{BC}$+$\overrightarrow{AD}$ | C. | $\overrightarrow{AC}$+$\overrightarrow{DB}$=$\overrightarrow{DC}$+$\overrightarrow{BA}$ | D. | $\overrightarrow{AB}$+$\overrightarrow{DA}$=$\overrightarrow{AC}$+$\overrightarrow{DB}$ |
16.2015年12月7日,北京首次启动空气重污染红色预警.其应急措施包括:全市范围内将实施机动车单双号限行(即单日只有单号车可以上路行驶,双日只有双号车可以上路行驶),其中北京的公务用车在单双号行驶的基础上,再停驶车量总数的30%.现某单位的公务车,职工的私家车数量如下表:
根据应急措施,12月8日,这个单位需要停驶的公务车和私家车一共有( )
| 公务车 | 私家车 | |
| 单号(辆) | 10 | 135 |
| 双号(辆) | 20 | 120 |
| A. | 154 辆 | B. | 149辆 | C. | 145辆 | D. | 140辆 |
17.若点P(x0,y0)在圆C:x2+y2=r2的内部,则直线xx0+yy0=r2与圆C的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 无法确定 |
