题目内容
17．若点P（x0，y0）在圆C：x2+y2=r2的内部，则直线xx0+yy0=r2与圆C的位置关系是（ ）| A． | 相交 | B． | 相切 | C． | 相离 | D． | 无法确定 |
分析 先利用点到直线的距离，求得圆心到直线x0x+y0y=r2的距离，根据P在圆内，判断出x02+y02＜r2，进而可知d＞r，故可知直线和圆相离．
解答 解：圆心O（0，0）到直线x0x+y0y=r2的距离为d=$\frac{{r}^{2}}{\sqrt{{{x}_{0}}^{2}+{{y}_{0}}^{2}}}$
∵点P（x0，y0）在圆内，∴x02+y02＜r2，则有d＞r，
故直线和圆相离．
故选：C．
点评 本题的考点是直线与圆的位置关系，主要考查了直线与圆的位置关系．考查了数形结合的思想，直线与圆的位置关系的判定．解题的关键是看圆心到直线的距离与圆的半径的大小关系．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
8．将函数f（x）=2sin（2x-$\frac{π}{3}$）的图象向左平移$\frac{π}{4}$个单位，得到函数g（x）的图象，则函数g（x）的一个单调递减区间是（ ）
| A． | [-$\frac{5π}{12}$，0] | B． | [-$\frac{π}{3}$，0] | C． | [0，$\frac{π}{3}$] | D． | [$\frac{π}{6}$，$\frac{π}{2}$] |
9．已知A（4，0）、B（0，5）是椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1的两个顶点，C是椭圆上处于第一象限内的点，则△ABC面积的最大值为（ ）
| A． | 10（$\sqrt{3}$-1） | B． | 10（$\sqrt{2}$+1） | C． | 10（$\sqrt{2}$-1） | D． | 10（$\sqrt{3}$+1） |
6．
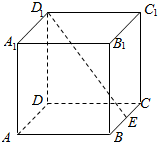姐图，在正方体ABCD-A1B1C1D1中，E为BC的中点，点P在正方体表面上移动，且满足B1P⊥D1E，则点B1和点P构成的图形是（ ）
姐图，在正方体ABCD-A1B1C1D1中，E为BC的中点，点P在正方体表面上移动，且满足B1P⊥D1E，则点B1和点P构成的图形是（ ）| A． | 三角形 | B． | 四边形 | C． | 曲边形 | D． | 五边形 |