Question

9．在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为直角梯形，∠CDA=∠BAD=90°，AD=DC=$\sqrt{2}$，AB=PA=2$\sqrt{2}$，且E为线段PB上的一动点．
（1）若E为线段PB的中点，求证：CE∥平面PAD；
（2）当直线CE与平面PAC所成角小于$\frac{π}{3}$，求PE长度的取值范围．

Answer 1

分析 （1）取PA的中点F，连结EF，DF，证明四边形EFDC是平行四边形得出CE∥DF，故而CE∥平面PAD；
（2）证明BC⊥平面PAC，可知∠PCE为CE与平面PAC所成的角，利用余弦定理得出∠BPC，利用勾股定理得出PE的最大值即可得出PE的范围．

解答 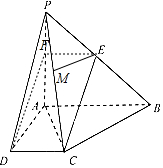证明：（1）取PA的中点F，连结EF，DF，
则EF∥AB，EF=$\frac{1}{2}$AB，
又DC∥AB，DC=$\frac{1}{2}$AB，
∴EF∥CD，EF=DC，
∴四边形EFDC是平行四边形，
∴CE∥DF，又CE?平面PAD，DF?平面PAD，
∴CE∥平面PAD．
解：（2）∵AD=CD=$\sqrt{2}$，AD⊥CD，∴AC=2，
又AB=2$\sqrt{2}$，∠BAC=45°，∴BC=2，
∴AC⊥BC，
又PA⊥平面ABCD，BC?平面ABCD，
∴PA⊥BC，又PA∩AC=A，
∴BC⊥平面PAC，
过E作EM∥BC，则EM⊥平面PAC，
∴∠PCE为CE与平面PAC所成的角，即∠PCE＜$\frac{π}{3}$．
∵PA=2$\sqrt{2}$，AC=2，∴PC=2$\sqrt{3}$，BC=2，PB=4，
∴∠BPC=$\frac{π}{6}$，
∴当∠PCE=$\frac{π}{3}$时，CE⊥PB，此时PE=3，
∴当∠PCE$＜\frac{π}{3}$时，PE＜3．

点评 本题考查了线面平行的判定，线面垂直的判定，属于中档题．