题目内容
已知函数y=2sin(
x-
).
(1)求此函数的单调递减区间.
(2)求它的最值以及取得最值是自变量x的取值集合.
| 1 |
| 2 |
| π |
| 4 |
(1)求此函数的单调递减区间.
(2)求它的最值以及取得最值是自变量x的取值集合.
考点:正弦函数的单调性,正弦函数的定义域和值域
专题:三角函数的图像与性质
分析:(1)根据三角函数的图象和性质即可求此函数的单调递减区间.
(2)根据三角函数的图象和性质即可求出函数的最值.
(2)根据三角函数的图象和性质即可求出函数的最值.
解答:
解:(1)由2kπ+
≤
x-
≤4kπ+
,
即4kπ+
≤x≤4kπ+
,(k∈Z)
即函数的单调递减区间是[4kπ+
,4kπ+
](k∈Z).
(2)当sin(
x-
)=1时,函数取得最大值2,此时x=4kπ+
,
当sin(
x-
)=-1时,函数取得最小值-2,此时x=4kπ+
,
故y最大值为2,此时x的取值集合{x|x=4kπ+
}(k∈Z)
y最小值=-2,此时x的取值集合{x|x=4kπ+
}(k∈Z).
| π |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
即4kπ+
| 3π |
| 2 |
| 7π |
| 2 |
即函数的单调递减区间是[4kπ+
| 3π |
| 2 |
| 7π |
| 2 |
(2)当sin(
| 1 |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
当sin(
| 1 |
| 2 |
| π |
| 4 |
| 7π |
| 2 |
故y最大值为2,此时x的取值集合{x|x=4kπ+
| 3π |
| 2 |
y最小值=-2,此时x的取值集合{x|x=4kπ+
| 7π |
| 2 |
点评:本题主要考查三角函数的图象和性质,考查三角函数的单调性和最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知中心在原点的双曲线C的左焦点为F1(-2,0),离心率e=2,则C的标准方程是( )
A、x2-
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=lnx+
的零点所在的区间是( )
| 1 |
| 2 |
| A、(e-4,e-2) |
| B、(e-2,1) |
| C、(1,e2) |
| D、(e2,e4) |
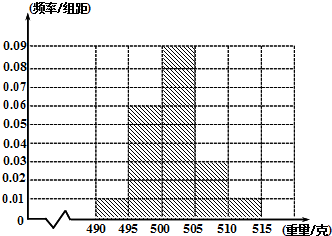 某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.