题目内容
用解析法证明：如果四边形ABCD是长方形，则对任一点M，等式|AM|2+|CM|2=|BM|2+|DM|2成立．
考点：两点间距离公式的应用
专题：直线与圆
分析：通过建立直角坐标系，设出长方形的顶点坐标，以及M的坐标，利用两点间距离公式求解即可．
解答：
解：以点A为原点，AB为x轴，AD为y轴，建立直角坐标系．
设AB=a，AD=b，则A、B、C、D的坐标分别为：（0，0）、（a，0）、（a，b）、（0，b）．
设点M的坐标为（x，y），
则有：|AM|2+|CM|2=[x2+y2]+[（x-a）2+（y-b）2]；
|BM|2+|DM|2=[（x-a）2+y2]+[x2+（y-b）2]；
所以|AM|2+|CM|2=|BM|2+|DM|2．
设AB=a，AD=b，则A、B、C、D的坐标分别为：（0，0）、（a，0）、（a，b）、（0，b）．
设点M的坐标为（x，y），
则有：|AM|2+|CM|2=[x2+y2]+[（x-a）2+（y-b）2]；
|BM|2+|DM|2=[（x-a）2+y2]+[x2+（y-b）2]；
所以|AM|2+|CM|2=|BM|2+|DM|2．
点评：本题考查解析法证明平面几何问题，注意坐标系的选取是解题的关键．
练习册系列答案
相关题目
下列推理过程是类比推理的是（ ）
A、人们通过大量试验得出掷硬币出现正面的概率为
| ||
| B、科学家通过研究老鹰的眼睛发明了电子鹰眼 | ||
| C、通过检测溶液的pH值得出溶液的酸碱性 | ||
| D、数学中由周期函数的定义判断某函数是否为周期函数 |
执行如图所示的程序框图所表达的算法，输出的结果为（ ）
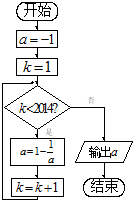
| A、2 | ||
| B、1 | ||
C、
| ||
| D、-1 |
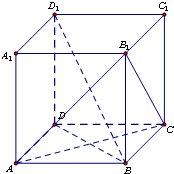已知正方体ABCD-A1B1C1D1中，求证：