题目内容

3．在区间[0，1]上随机地取两个数x，y组成点P（x，y），求满足x2+y2≤1的事件概率．

分析 该题涉及两个变量，故是与面积有关的几何概型，分别表示出满足条件的面积和整个区域的面积，最后利用概率公式解之即可．

解答 解：由题意可得$\left\{\begin{array}{l}{0≤x≤1}\\{0≤y≤1}\end{array}\right.$的区域为边长为1的正方形，面积为1，
∵x2+y2≤1的区域是圆的内部的阴影区域，其面积S=$\frac{1}{4}$π，
∴在区间[0，1]上随机地取两个数x，y组成点P（x，y），求满足x2+y2≤1的事件概率为$\frac{π}{4}$

点评 本题主要考查了与面积有关的几何概率的求解，解题的关键是准确求出区域的面积，属于中档题

练习册系列答案
相关题目
13．已知f（x）=|lnx|，设0＜a＜b，且f（a）=f（b），则a+2b的取值范围是（　　）
A．[3，+∞）B．（3，+∞）C．$[2\sqrt{2}，+∞）$D．$（2\sqrt{2}，+∞）$
14．①命题“若b2-4ac＜0，则方程ax2+bx+c=0（a≠0）无实根”的否命题为真命题；
②命题“?x∈N，x3＞x2”的否定是“?x0∈N，使x${\;}_{0}^{3}$＞x${\;}_{0}^{2}$”；
③“b=0”是“函数f（x）=ax2+bx+c为偶函数”的充要条件；
④“正四棱锥的底面是正方形”的逆命题为真命题；
⑤a＞1是（a-2）（a-1）＞0的必要不充分条件．
其中正确命题的序号是①③．
11．x2+（y+2）2=3的圆心坐标、半径分别为（　　）
A．（0，2）；3B．（0，-2）；3C．$（{0，2}）；\sqrt{3}$D．$（{0，-2}）；\sqrt{3}$
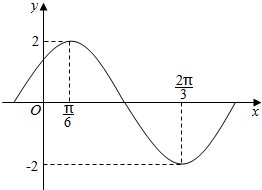18．圆A：x2+y2+4x+2y+1=0与圆B：x2+y2-2x-6y+1=0的位置关系是外切．
8．设-$\sqrt{2}$≤a≤$\sqrt{2}$，b≠0，a，b∈R，则（a-b）2+（$\sqrt{2-{a}^{2}}$-$\frac{9}{b}$）2的最小值为8．
15．函数$f（x）=Asin（ωx+φ）\;（A＞0，ω＞0，|φ|＜\frac{π}{2}）$部分图象如图所示．
（Ⅰ）求f（x）的最小正周期及解析式；
（Ⅱ）求函数f（x）的单调递减区间；
（Ⅲ）设g（x）=f（x）-2cos2x，求函数g（x）在区间$[0，\frac{π}{2}]$上的值域．
12．计算题
（1）求值：${27^{\frac{2}{3}}}-{（{\root{3}{-125}}）^2}-{2^{{{log}_2}3}}×{log_2}\frac{1}{8}+{log_2}3×{log_3}4$
（2）求不等式的解集：①33-x＜2；②${log_5}（{x-1}）＜\frac{1}{2}$．
13．已知$\frac{π}{2}$＜β＜α＜$\frac{3π}{4}$，cos（α-β）=$\frac{12}{13}$，sin（α+β）=-$\frac{3}{5}$，求sin2β的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网