题目内容
15.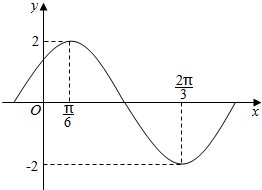 函数$f(x)=Asin(ωx+φ)\;(A>0,ω>0,|φ|<\frac{π}{2})$部分图象如图所示.
函数$f(x)=Asin(ωx+φ)\;(A>0,ω>0,|φ|<\frac{π}{2})$部分图象如图所示.(Ⅰ)求f(x)的最小正周期及解析式;
(Ⅱ)求函数f(x)的单调递减区间;
(Ⅲ)设g(x)=f(x)-2cos2x,求函数g(x)在区间$[0,\frac{π}{2}]$上的值域.
分析 (Ⅰ)由函数图象观察可知A,函数的周期T=2($\frac{2π}{3}$-$\frac{π}{6}$)=π,由周期公式可得ω,由点($\frac{π}{6}$,2)在函数图象上,解得φ=2kπ+$\frac{π}{6}$,k∈Z结合范围|φ|≤$\frac{π}{2}$,求得φ的值,从而可得函数解析式;
(Ⅱ)令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z,即可解得函数f(x)的单调递减区间.
(Ⅲ)先求g(x)=2sin(2x-$\frac{π}{6}$),当x∈$[0,\frac{π}{2}]$时,可求2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],利用正弦函数的性质可得所求值域.
解答 解:由函数图象观察可知:A=2…(1分),
函数的周期T=2($\frac{2π}{3}$-$\frac{π}{6}$)=π,由周期公式可得:ω=$\frac{2π}{ω}$=2…(2分)
由点($\frac{π}{6}$,2)在函数图象上,可得:2sin(2×$\frac{π}{6}$+φ)=2,可得:φ=2kπ+$\frac{π}{6}$,k∈Z
∵|φ|≤$\frac{π}{2}$,
∴φ=$\frac{π}{6}$…(4分)
∴f(x)的解析式为:f(x)=2sin(2x+$\frac{π}{6}$).
(Ⅱ)令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z,即可解得函数f(x)的单调递减区间为:[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z.…(7分)
(Ⅲ)∵g(x)=f(x)-2cos2x=2sin(2x+$\frac{π}{6}$)-2cos2x=$\sqrt{3}$sin2x-cos2x=2sin(2x-$\frac{π}{6}$),…(9分)
∴当x∈$[0,\frac{π}{2}]$时,2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],可得:sin(2x-$\frac{π}{6}$)∈[-$\frac{1}{2}$,1].
∴函数g(x)=2sin(2x-$\frac{π}{6}$)在区间$[0,\frac{π}{2}]$上的值域为:[-1,2].…(12分)
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了正弦函数的图象和性质,考查了计算能力,属于基本知识的考查.

| A. | 命题“若x2-5x+6=0,则x=2”的逆命题是“若x≠2,则x2-5x+6≠0” | |
| B. | 命题“若x=2,则x2-5x+6=0”的否命题是“若x=2,则x2-5x+6≠0” | |
| C. | 已知a,b∈R,命题“若a>b,则|a|>|b|”的逆否命题是真命题 | |
| D. | 若a,b∈R,则“ab≠0”是“a≠0”的充分条件 |
| A. | y=3x-2 | B. | y=3x2-1 | C. | y=2x2+3x | D. | y=$\frac{2}{x}$-1 |