题目内容
19.已知各项均为正数的等比数列{an}中,$3{a_1},\frac{1}{2}{a_3},2{a_2}$成等差数列,则$\frac{{{a_{11}}+{a_{13}}}}{{{a_8}+{a_{10}}}}$=( )| A. | 27 | B. | -1或27 | C. | 3 | D. | -1或3 |
分析 设各项均为正数的等比数列{an}的公比为q>0,由$3{a_1},\frac{1}{2}{a_3},2{a_2}$成等差数列,可得$2×\frac{1}{2}{a}_{3}$=3a1+2a2,化为:${a}_{1}{q}^{2}$=3a1+2a1q,解得q.利用$\frac{{{a_{11}}+{a_{13}}}}{{{a_8}+{a_{10}}}}$=$\frac{{q}^{3}({a}_{8}+{a}_{10})}{{a}_{8}+{a}_{10}}$,即可得出.
解答 解:设各项均为正数的等比数列{an}的公比为q>0,∵$3{a_1},\frac{1}{2}{a_3},2{a_2}$成等差数列,
∴$2×\frac{1}{2}{a}_{3}$=3a1+2a2,化为:${a}_{1}{q}^{2}$=3a1+2a1q,即q2-2q-3=0,解得q=3.
则$\frac{{{a_{11}}+{a_{13}}}}{{{a_8}+{a_{10}}}}$=$\frac{{q}^{3}({a}_{8}+{a}_{10})}{{a}_{8}+{a}_{10}}$=33=27.
点评 本题考查了等差数列与等比数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.执行如图所示的程序框图,则输出结果s的值为( )


| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 0 |
10.$\int_{0}^{π}{({cosx+1})}dx$等于( )
| A. | 1 | B. | 0 | C. | π | D. | π+1 |
7.已知f(x)=5x5+4x4+3x3+2x2+x+1,若用秦九韶算法求f(5)的值,下面说法正确的是( )
| A. | 至多4乘法运算和5次加法运算 | B. | 15次乘法运算和5次加法运算 | ||
| C. | 10次乘法运算和5次加法运算 | D. | 至多5次乘法运算和5次加法运算 |
14.执行如图所示的程序框图,若输入x=2,则输出y的值为( )
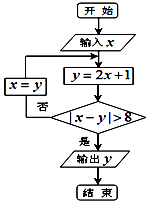

| A. | 5 | B. | 11 | C. | 23 | D. | 47 |
11.若a∈R,则“a>0”是“a+$\frac{1}{a}$≥2”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
8.口袋中有5个形状和大小完全相同的小球,编号分别为0,1,2,3,4,从中任取3个球,以ξ表示取出球的最小号码,则Eξ=( )
| A. | 0.45 | B. | 0.5 | C. | 0.55 | D. | 0.6 |
9.方程(x2+y2-2)$\sqrt{x-3}$=0表示的曲线是( )
| A. | 一个圆和一条直线 | B. | 一个圆和一条射线 | ||
| C. | 一个圆 | D. | 一条直线 |
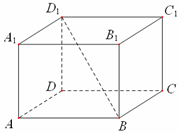 如图,在正四棱柱ABCD-A1B1C1D1中,底面ABCD的边长为7,BD1与底面所成角的大小为$arctan\frac{6}{7}$,则该正四棱柱的高等于$6\sqrt{2}$.
如图,在正四棱柱ABCD-A1B1C1D1中,底面ABCD的边长为7,BD1与底面所成角的大小为$arctan\frac{6}{7}$,则该正四棱柱的高等于$6\sqrt{2}$.