Question

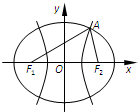如图，F₁，F₂是双曲线C₁：x²-

y2

3

=1与椭圆C₂的公共焦点，点A是C₁，C₂在第一象限的公共点．若|F₁F₂|=|F₁A|，则C₂的离心率是（　　）

• A、

  1

  3

• B、

  2

  3

• C、

  1

  5

• D、

  2

  5

Answer 1

考点：双曲线的简单性质

专题：计算题,圆锥曲线的定义、性质与方程

分析：利用双曲线的定义，可求出|F₂A|=2，|F₁F₂|=4，进而有|F₁A|+|F₂A|=6，由此可求C₂的离心率．

解答： 解：由题意知，|F₁F₂|=|F₁A|=4，
∵|F₁A|-|F₂A|=2，
∴|F₂A|=2，
∴|F₁A|+|F₂A|=6，
∵|F₁F₂|=4，
∴C₂的离心率是

4

6

=

2

3

．
故选B．

点评：本题考查椭圆、双曲线的几何性质，考查学生的计算能力，正确运用椭圆、双曲线的几何性质是关键．