题目内容
P是椭圆
+
=1上的一点,F1和F2是焦点,若∠F1PF2=60°,则△PF1F2的面积为( )
| x2 |
| 100 |
| y2 |
| 64 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:综合题,解三角形,圆锥曲线的定义、性质与方程
分析:根据椭圆的定义,得PF1+PF2=2a=20…①,再在△F1PF2中用余弦定理,得PF12+PF22-PF1•PF2=144…②.由①②联解,得PF1•PF2,最后用根据正弦定理关于面积的公式,可得△PF1F2的面积.
解答:
解:∵椭圆
+
=1,
∴a2=100,b2=64.可得a=10,c2=100-64=36,即c=6.
∵P是椭圆
+
=1的一点,F1、F2是焦点,
∴根据椭圆的定义,得PF1+PF2=2a=20…①
又∵△F1PF2中,∠F1PF2=60°且F1F2=2c=12,
∴根据余弦定理,得F1F22=PF12+PF22-2PF1•PF2cos60°=144
即PF12+PF22-PF1•PF2=144…②
∴①②联解,得PF1•PF2=
,
根据正弦定理,得△PF1F2的面积为:S=
PF1•PF2sin60°=
.
故选B.
| x2 |
| 100 |
| y2 |
| 64 |
∴a2=100,b2=64.可得a=10,c2=100-64=36,即c=6.
∵P是椭圆
| x2 |
| 100 |
| y2 |
| 64 |
∴根据椭圆的定义,得PF1+PF2=2a=20…①
又∵△F1PF2中,∠F1PF2=60°且F1F2=2c=12,
∴根据余弦定理,得F1F22=PF12+PF22-2PF1•PF2cos60°=144
即PF12+PF22-PF1•PF2=144…②
∴①②联解,得PF1•PF2=
| 256 |
| 3 |
根据正弦定理,得△PF1F2的面积为:S=
| 1 |
| 2 |
64
| ||
| 3 |
故选B.
点评:本题给出椭圆上一点对两个焦点的张角为60°,求椭圆两焦点与该点构成三角形的面积,着重考查了椭圆的简单性质和正弦定理等知识点,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
球的半径扩大到原来的2倍,则它的体积扩大到原来的( )
| A、2倍 | B、4倍 | C、6倍 | D、8倍 |
已知双曲线
-
=1的一个焦点与抛物线y2=-4x的焦点重合,且双曲线的离心率为
,则此双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
A、5x2-
| ||||
B、5x2-
| ||||
C、
| ||||
D、
|
过原点的直线与圆x2+y2-4y+3=0相切,若切点在第二象限,则该直线的方程是( )
A、y=
| ||||
B、y=
| ||||
C、y=-
| ||||
D、y=-
|
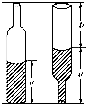 如图,啤酒瓶的高为h,瓶内酒面高度为a,若将瓶盖盖好倒置,酒面高度为a′(a′+b=h),则酒瓶容积与瓶内酒的体积之比为( )
如图,啤酒瓶的高为h,瓶内酒面高度为a,若将瓶盖盖好倒置,酒面高度为a′(a′+b=h),则酒瓶容积与瓶内酒的体积之比为( )A、1+
| ||
B、1+
| ||
C、1+
| ||
D、1+
|
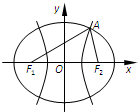 如图,F1,F2是双曲线C1:x2-
如图,F1,F2是双曲线C1:x2-