题目内容
在△ABC中,若lg(a+c)+lg(a-c)=lgb-lg
,则A=( )
| 1 |
| b+c |
| A、90° | B、60° |
| C、120° | D、150° |
考点:对数的运算性质
专题:计算题
分析:由对数的运算性质得到三角形三边的关系,结合余弦定理求解角A的值.
解答:
解:由lg(a+c)+lg(a-c)=lgb-lg
,得
(a+c)(a-c)=b(b+c),
即a2-c2=b2+bc,
b2+c2-a2=-bc,
根据余弦定理得:cosA=
=
=-
.
又0°<A<180°,
∴A=120°.
故选:C.
| 1 |
| b+c |
(a+c)(a-c)=b(b+c),
即a2-c2=b2+bc,
b2+c2-a2=-bc,
根据余弦定理得:cosA=
| b2+c2-a2 |
| 2bc |
| -bc |
| 2bc |
| 1 |
| 2 |
又0°<A<180°,
∴A=120°.
故选:C.
点评:本题考查了对数的运算性质,考查了余弦定理的应用,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
直线4x+3y=0与圆(x-1)2+(y-2)2=16的位置关系是( )
| A、相离 | B、相切 |
| C、相交但不过圆心 | D、相交过圆心 |
球的半径扩大到原来的2倍,则它的体积扩大到原来的( )
| A、2倍 | B、4倍 | C、6倍 | D、8倍 |
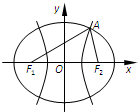 如图,F1,F2是双曲线C1:x2-
如图,F1,F2是双曲线C1:x2-