题目内容
若实数x、y满足等式 (x-2)2+y2=3,那么x+2y的最大值为 .
考点:直线与圆的位置关系
专题:直线与圆
分析:令t=x+2y,则y=-
x+
表示过圆上一点的直线.且当直线在y轴上截距最大时,x+2y有最大值.画出满足等式(x-2)2+y2=3的图形,由数形结合,我们易求出x+2y的最大值.
| 1 |
| 2 |
| t |
| 2 |
解答:
 解:令t=x+2y,
解:令t=x+2y,
则y=-
x+
.
当直线在y轴上截距最大时,x+2y有最大值.
又∵直线过圆上一点
由图可得,当直线与圆相切并且切点在第一象限时,
直线在y轴上的截距最大,此时x+2y取最大值.
∴圆心到直线的距离
d=
=
∴t=2±
又∵切点在第一象限
∴t=2+
此时,x+2y=2+
所以,x+2y的最大值为2+
.
 解:令t=x+2y,
解:令t=x+2y,则y=-
| 1 |
| 2 |
| t |
| 2 |
当直线在y轴上截距最大时,x+2y有最大值.
又∵直线过圆上一点
由图可得,当直线与圆相切并且切点在第一象限时,
直线在y轴上的截距最大,此时x+2y取最大值.
∴圆心到直线的距离
d=
| |2-t| | ||
|
| 3 |
∴t=2±
| 15 |
又∵切点在第一象限
∴t=2+
| 15 |
此时,x+2y=2+
| 15 |
所以,x+2y的最大值为2+
| 15 |
点评:本题考查的知识点是简单线性规划,分析出直线在y轴上截距最大时,x+2y有最大值是解答本题的关键.

练习册系列答案
相关题目
过原点的直线与圆x2+y2-4y+3=0相切,若切点在第二象限,则该直线的方程是( )
A、y=
| ||||
B、y=
| ||||
C、y=-
| ||||
D、y=-
|
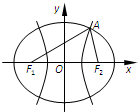 如图,F1,F2是双曲线C1:x2-
如图,F1,F2是双曲线C1:x2-