题目内容
若动点P与定点F(1,1)的距离和动点P与直线l:3x+y-4=0的距离相等,则动点P的轨迹方程是 .
考点:轨迹方程
专题:计算题,直线与圆
分析:判断定点F与直线的位置关系,然后判断动点的轨迹,即可求出方程.
解答:
解:因为定点F(1,1)在直线l:3x+y-4=0上,
所以到定点F的距离和到定直线l的距离相等的点的轨迹是直线,
就是经过定点F与直线l:3x+y-4=0垂直的直线.
所以动点P的轨迹方程是y-1=
(x-1),即x-3y+2=0.
故答案为:x-3y+2=0.
所以到定点F的距离和到定直线l的距离相等的点的轨迹是直线,
就是经过定点F与直线l:3x+y-4=0垂直的直线.
所以动点P的轨迹方程是y-1=
| 1 |
| 3 |
故答案为:x-3y+2=0.
点评:本题考查动点的轨迹方程的求法,逻辑推理能力,考查计算能力.注意本题与抛物线定义的区别.

练习册系列答案
相关题目
问题:①有1000盒生产批次不同的药品,第一批500盒,第二批200盒,第三批300盒,现从中抽取一个容量为100的样本;②从20名学生中选出3名参加座谈会.方法:1.简单随机抽样法;2.系统抽样法;3.分层抽样法.其中问题与方法的最佳配对是( )
| A、①1,②2 |
| B、①3,②1 |
| C、①2,②3 |
| D、①3,②2 |
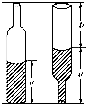 如图,啤酒瓶的高为h,瓶内酒面高度为a,若将瓶盖盖好倒置,酒面高度为a′(a′+b=h),则酒瓶容积与瓶内酒的体积之比为( )
如图,啤酒瓶的高为h,瓶内酒面高度为a,若将瓶盖盖好倒置,酒面高度为a′(a′+b=h),则酒瓶容积与瓶内酒的体积之比为( )A、1+
| ||
B、1+
| ||
C、1+
| ||
D、1+
|
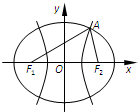 如图,F1,F2是双曲线C1:x2-
如图,F1,F2是双曲线C1:x2-