题目内容
10.如图△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积为6
分析 根据斜二侧画法得到三角形OAB的底面边长OB=3,高OA=2O'A'=4,问题得以解决
解答 解:根据斜二侧画法得到三角形OAB为直角三角形,底面边长OB=3,高OA=2O'A'=4,
所以:S△OAB=$\frac{1}{2}$×3×4=6,
故答案为:6.
点评 本题主要考查平面图形的直观图的应用,要求熟练掌握斜二测画法的边长关系,比较基础.

练习册系列答案
相关题目
1.已知i是虚数单位,复数z满足z=i(i-1),则z的虚部是( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
18.在△ABC中,a,b,c分别为三个内角A、B、C所对的,若$cosB=\frac{1}{4},b=2,sinC=2sinA$,则△ABC的面积为( )
| A. | $\frac{{\sqrt{15}}}{6}$ | B. | $\frac{{\sqrt{15}}}{4}$ | C. | $\frac{{\sqrt{15}}}{2}$ | D. | $\sqrt{15}$ |
15.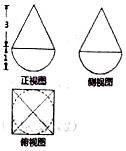 一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
 一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )| A. | $4+\frac{2π}{3}$ | B. | $4+\frac{{\sqrt{2}π}}{6}$ | C. | $2+\frac{2π}{3}$ | D. | $2+\frac{{\sqrt{2}π}}{6}$ |
2.如图,△A'B'C'是△ABC的直观图,其中A'B'=A'C',那么△ABC是( )
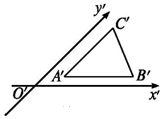

| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
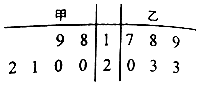 甲、乙两名技工在相同的条件下生产某种零件,连续6天中,他们日加工的合格零件数的统计数据的茎叶图,如图所示.
甲、乙两名技工在相同的条件下生产某种零件,连续6天中,他们日加工的合格零件数的统计数据的茎叶图,如图所示.