题目内容
5.已知圆C:x2+y2=4上恰有两个点到直线l:x-y+m=0的距离都等于1,则实数m的取值范围是( )| A. | $[{-3\sqrt{2},-\sqrt{2}})∪({\sqrt{2},3\sqrt{2}}]$ | B. | $({-3\sqrt{2},-\sqrt{2}}]∪[{\sqrt{2},3\sqrt{2}})$ | C. | $[{-3\sqrt{2},-\sqrt{2}}]∪[{\sqrt{2},3\sqrt{2}}]$ | D. | $({-3\sqrt{2},-\sqrt{2}})∪({\sqrt{2},3\sqrt{2}})$ |
分析 若圆x2+y2=4上恰有2个点到直线l的距离等于1,则满足O到直线l:x-y+m=0的距离1<d<3,代入点到直线的距离公式,可得答案.
解答 解:由圆C的方程:x2+y2=4,可得圆C的圆心为原点O(0,0),半径为2
若圆x2+y2=4上恰有2个点到直线l的距离等于1,则满足O到直线l:x-y+m=0的距离1<d<3,
∵直线l的一般方程为:x-y+m=0,
∴1<$\frac{|m|}{\sqrt{2}}$<3,
解得-3$\sqrt{2}$<m<-$\sqrt{2}$或$\sqrt{2}$<m<3$\sqrt{2}$,
故选:D.
点评 本题考查直线与圆的位置关系,考查点到直线的距离公式,其中分析出O到直线l:x-y+m=0的距离是解答的关键.

练习册系列答案
相关题目
16.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{2}x|,0<x≤2}\\{2-lo{g}_{2}x,x>2}\end{array}\right.$若a,b,c互不相等,且f(a)=f(b)=f(c),则ab+bc+ca的取值范围是( )
| A. | (1,4) | B. | (2,4) | C. | (6,9) | D. | (7,9) |
20.已知点M(a,b,c)是空间直角坐标系O-xyz中的一点,则与点M关于z轴对称的点的坐标是( )
| A. | (a,-b,-c) | B. | (-a,b,-c) | C. | (-a,-b,c) | D. | (-a,-b,-c) |
10.经过两点$A({-1,\sqrt{3}})$,$B({1,-\sqrt{3}})$的直线的倾斜角为( )
| A. | 120° | B. | 150° | C. | 60° | D. | 30° |
14.已知p:x2-2x-3<0,q:x+2≥0,则p是q的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.惫设f(x)=-m(m+e)x2,g(x)=x2+(m-1)x-m,其中e均自然对数的底数,若?x∈R,使得f(x)<0或g(x)<0,则实数m的取值范围是( )
| A. | {m|-e≤m≤0} | B. | {m|0≤m≤e} | C. | {m∈R|m≠-1} | D. | {-1} |
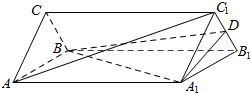 如图,底面为正三角形的三棱柱ABC-A1B1C1中,侧棱垂直于底面,D为线段B1C1中点.
如图,底面为正三角形的三棱柱ABC-A1B1C1中,侧棱垂直于底面,D为线段B1C1中点.