题目内容
16.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{2}x|,0<x≤2}\\{2-lo{g}_{2}x,x>2}\end{array}\right.$若a,b,c互不相等,且f(a)=f(b)=f(c),则ab+bc+ca的取值范围是( )| A. | (1,4) | B. | (2,4) | C. | (6,9) | D. | (7,9) |
分析 画出函数f(x)的图象,设a<b<c,可得0<a<1<b<2<c<4,再由条件去掉绝对值,运用对数的运算性质,可得ab=1,bc=4,log2a=log2c-2,即有ab+bc+ac=ac+5,求得log2(ac)的范围,即可得到所求范围.
解答 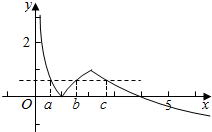 解:画出函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{2}x|,0<x≤2}\\{2-lo{g}_{2}x,x>2}\end{array}\right.$的图象,
解:画出函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{2}x|,0<x≤2}\\{2-lo{g}_{2}x,x>2}\end{array}\right.$的图象,
设a<b<c,可得0<a<1<b<2<c<4,
由f(a)=f(b)=f(c),
可得|log2a|=|log2b|=2-log2c,
即为-log2a=log2b=2-log2c,
即log2a+log2b=0,log2b+log2c=2,log2a=log2c-2,
即有ab=1,bc=4,
则ab+bc+ca=1+4+ac=ac+5,
由于log2(ac)=log2a+log2c=2log2c-2,
由2<c<4,可得0<2log2c-2<2,
即有1<ac<4,即6<ac+5<9.
故选C.
点评 本题考查分段函数的运用,考查对数函数的图象和运用,注意运用数形结合的思想方法和对数函数的单调性和运算性质,属于中档题.

练习册系列答案
相关题目
4.已知$\overrightarrow{a}=(-3,2,5)$,$\overrightarrow{b}=(1,m,3)$,若$\overrightarrow{a}⊥\overrightarrow{b}$,则常数m=( )
| A. | -6 | B. | 6 | C. | -9 | D. | 9 |
11.若命题“p且q”为假,且“?p”为假,则( )
| A. | “p或q”为假 | B. | q假 | C. | q真 | D. | p假 |
1.与函数y=$\frac{1}{\sqrt{x-1}}$的定义域相同的函数是( )
| A. | y=$\sqrt{x-1}$ | B. | y=2x-1 | C. | y=$\frac{1}{x-1}$ | D. | y=ln(x-1) |
5.已知圆C:x2+y2=4上恰有两个点到直线l:x-y+m=0的距离都等于1,则实数m的取值范围是( )
| A. | $[{-3\sqrt{2},-\sqrt{2}})∪({\sqrt{2},3\sqrt{2}}]$ | B. | $({-3\sqrt{2},-\sqrt{2}}]∪[{\sqrt{2},3\sqrt{2}})$ | C. | $[{-3\sqrt{2},-\sqrt{2}}]∪[{\sqrt{2},3\sqrt{2}}]$ | D. | $({-3\sqrt{2},-\sqrt{2}})∪({\sqrt{2},3\sqrt{2}})$ |
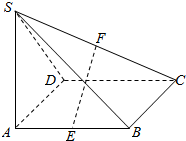 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.