题目内容
15.函数y=x2+4x-1的递增区间是(-2,+∞).分析 根据二次函数的开口方向和对称轴可判断出在对称轴右侧单调递增.
解答 解:∵函数y=x2+4x-1的图象开口向上,对称轴为x=-2,
∴y=x2+4x-1在(-∞,-2)上单调递减,在(-2,+∞)上单调递增.
故答案为(-2,+∞).
点评 本题考查了二次函数的单调性与对称轴的关系,属于基础题.

练习册系列答案
相关题目
5.某城市有甲、乙两种报纸供居民们订阅,记事件A为“只订阅甲报纸”,事件B为“至少订一种报纸”,事件C为“至多订一种报纸”,事件D为“不订甲报纸”,事件E为“一种报纸也不订”.下列是对立事件的是( )
| A. | A与C | B. | B与E | C. | B与C | D. | C与E |
4.已知$\overrightarrow{a}=(-3,2,5)$,$\overrightarrow{b}=(1,m,3)$,若$\overrightarrow{a}⊥\overrightarrow{b}$,则常数m=( )
| A. | -6 | B. | 6 | C. | -9 | D. | 9 |
5.已知圆C:x2+y2=4上恰有两个点到直线l:x-y+m=0的距离都等于1,则实数m的取值范围是( )
| A. | $[{-3\sqrt{2},-\sqrt{2}})∪({\sqrt{2},3\sqrt{2}}]$ | B. | $({-3\sqrt{2},-\sqrt{2}}]∪[{\sqrt{2},3\sqrt{2}})$ | C. | $[{-3\sqrt{2},-\sqrt{2}}]∪[{\sqrt{2},3\sqrt{2}}]$ | D. | $({-3\sqrt{2},-\sqrt{2}})∪({\sqrt{2},3\sqrt{2}})$ |
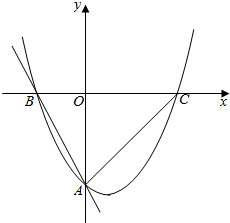 如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点
如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点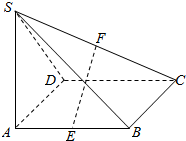 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.