题目内容
20.已知点M(a,b,c)是空间直角坐标系O-xyz中的一点,则与点M关于z轴对称的点的坐标是( )| A. | (a,-b,-c) | B. | (-a,b,-c) | C. | (-a,-b,c) | D. | (-a,-b,-c) |
分析 先根据空间直角坐标系对称点的特征,点(x,y,z)关于z轴的对称点的坐标为只须将横坐标、纵坐标变成原来的相反数即可,即可得对称点的坐标.
解答 解:∵在空间直角坐标系中,
点(x,y,z)关于z轴的对称点的坐标为:(-x,-y,z),
∴点M(a,b,c)关于z轴的对称点的坐标为:
(-a,-b,c).
故选:C.
点评 本小题主要考查空间直角坐标系、空间直角坐标系中点的坐标特征等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,属于基础题.

练习册系列答案
相关题目
11.若命题“p且q”为假,且“?p”为假,则( )
| A. | “p或q”为假 | B. | q假 | C. | q真 | D. | p假 |
5.已知圆C:x2+y2=4上恰有两个点到直线l:x-y+m=0的距离都等于1,则实数m的取值范围是( )
| A. | $[{-3\sqrt{2},-\sqrt{2}})∪({\sqrt{2},3\sqrt{2}}]$ | B. | $({-3\sqrt{2},-\sqrt{2}}]∪[{\sqrt{2},3\sqrt{2}})$ | C. | $[{-3\sqrt{2},-\sqrt{2}}]∪[{\sqrt{2},3\sqrt{2}}]$ | D. | $({-3\sqrt{2},-\sqrt{2}})∪({\sqrt{2},3\sqrt{2}})$ |
12.两条平行直线3x-4y+12=0与3x-4y-13=0间的距离为( )
| A. | $\frac{1}{5}$ | B. | $\frac{5}{2}$ | C. | $\frac{23}{5}$ | D. | 5 |
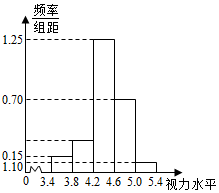 为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是2,则根据图中数据可得被样本数据在[3.8,4.2)内的人数是6.
为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是2,则根据图中数据可得被样本数据在[3.8,4.2)内的人数是6.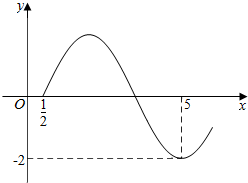 已知函数f(x)=2sin(ωx+φ)$({ω>0,-\frac{π}{2}<φ<0})$的图象如图所示.
已知函数f(x)=2sin(ωx+φ)$({ω>0,-\frac{π}{2}<φ<0})$的图象如图所示.