题目内容
14.已知p:x2-2x-3<0,q:x+2≥0,则p是q的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合不等式之间的关系进行判断即可.
解答 解:由x2-2x-3<0,得-1<x<3,
由x+2≥0得x≥-2,
则p是q的充分不必要条件,
故选:A
点评 本题主要考查充分条件和必要条件的判断,根据不等式之间的关系是解决本题的关键.比较基础.

练习册系列答案
相关题目
4.已知$\overrightarrow{a}=(-3,2,5)$,$\overrightarrow{b}=(1,m,3)$,若$\overrightarrow{a}⊥\overrightarrow{b}$,则常数m=( )
| A. | -6 | B. | 6 | C. | -9 | D. | 9 |
5.已知圆C:x2+y2=4上恰有两个点到直线l:x-y+m=0的距离都等于1,则实数m的取值范围是( )
| A. | $[{-3\sqrt{2},-\sqrt{2}})∪({\sqrt{2},3\sqrt{2}}]$ | B. | $({-3\sqrt{2},-\sqrt{2}}]∪[{\sqrt{2},3\sqrt{2}})$ | C. | $[{-3\sqrt{2},-\sqrt{2}}]∪[{\sqrt{2},3\sqrt{2}}]$ | D. | $({-3\sqrt{2},-\sqrt{2}})∪({\sqrt{2},3\sqrt{2}})$ |
2.某同学在求函数y=lgx和$y=\frac{1}{x}$的图象的交点时,计算出了下表所给出的函数值,则交点的横坐标在下列哪个区间内( )
| x | 2 | 2.125 | 2.25 | 2.375 | 2.5 | 2.625 | 2.75 | 2.875 | 3 |
| lgx | 0.301 | 0.327 | 0.352 | 0.376 | 0.398 | 0.419 | 0.439 | 0.459 | 0.477 |
| $\frac{1}{x}$ | 0.5 | 0.471 | 0.444 | 0.421 | 0.400 | 0.381 | 0.364 | 0.348 | 0.333 |
| A. | (2.125,2,25) | B. | (2.75,2.875) | C. | (2.625,2.75) | D. | (2.5,2.625) |
19.在△ABC中,a、b、c分别为角A、B、C所对的边,若B=60°,b2=ac,则△ABC的形状是( )
| A. | 直角三角形 | B. | 钝角三角形 | ||
| C. | 等腰非等边三角形 | D. | 等边三角形 |
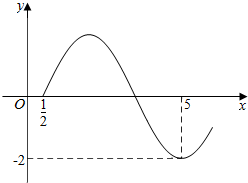 已知函数f(x)=2sin(ωx+φ)$({ω>0,-\frac{π}{2}<φ<0})$的图象如图所示.
已知函数f(x)=2sin(ωx+φ)$({ω>0,-\frac{π}{2}<φ<0})$的图象如图所示.