题目内容
10.经过两点$A({-1,\sqrt{3}})$,$B({1,-\sqrt{3}})$的直线的倾斜角为( )| A. | 120° | B. | 150° | C. | 60° | D. | 30° |
分析 设经过两点$A({-1,\sqrt{3}})$,$B({1,-\sqrt{3}})$的直线的倾斜角为θ,利用斜率计算公式可得:tanθ=$\frac{\sqrt{3}-(-\sqrt{3})}{-1-1}$,解出即可得出.
解答 解:设经过两点$A({-1,\sqrt{3}})$,$B({1,-\sqrt{3}})$的直线的倾斜角为θ,
则tanθ=$\frac{\sqrt{3}-(-\sqrt{3})}{-1-1}$=-$\sqrt{3}$,
∵θ∈[0°,180°),
∴θ=120°.
故选:A.
点评 本题考查了直线的倾斜角与斜率的关系、三角函数求值,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
1.与函数y=$\frac{1}{\sqrt{x-1}}$的定义域相同的函数是( )
| A. | y=$\sqrt{x-1}$ | B. | y=2x-1 | C. | y=$\frac{1}{x-1}$ | D. | y=ln(x-1) |
5.已知圆C:x2+y2=4上恰有两个点到直线l:x-y+m=0的距离都等于1,则实数m的取值范围是( )
| A. | $[{-3\sqrt{2},-\sqrt{2}})∪({\sqrt{2},3\sqrt{2}}]$ | B. | $({-3\sqrt{2},-\sqrt{2}}]∪[{\sqrt{2},3\sqrt{2}})$ | C. | $[{-3\sqrt{2},-\sqrt{2}}]∪[{\sqrt{2},3\sqrt{2}}]$ | D. | $({-3\sqrt{2},-\sqrt{2}})∪({\sqrt{2},3\sqrt{2}})$ |
2.某同学在求函数y=lgx和$y=\frac{1}{x}$的图象的交点时,计算出了下表所给出的函数值,则交点的横坐标在下列哪个区间内( )
| x | 2 | 2.125 | 2.25 | 2.375 | 2.5 | 2.625 | 2.75 | 2.875 | 3 |
| lgx | 0.301 | 0.327 | 0.352 | 0.376 | 0.398 | 0.419 | 0.439 | 0.459 | 0.477 |
| $\frac{1}{x}$ | 0.5 | 0.471 | 0.444 | 0.421 | 0.400 | 0.381 | 0.364 | 0.348 | 0.333 |
| A. | (2.125,2,25) | B. | (2.75,2.875) | C. | (2.625,2.75) | D. | (2.5,2.625) |
19.在△ABC中,a、b、c分别为角A、B、C所对的边,若B=60°,b2=ac,则△ABC的形状是( )
| A. | 直角三角形 | B. | 钝角三角形 | ||
| C. | 等腰非等边三角形 | D. | 等边三角形 |
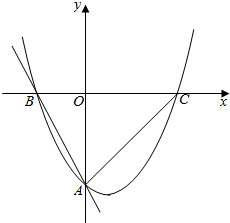 如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点
如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点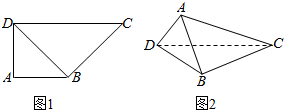 如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.
如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.