题目内容
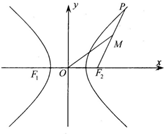 如图,双曲线
如图,双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,可得|OF2|=|F2M|=c,|MO|=2a+c,直线的倾斜角为60°,利用余弦定理,建立a,c的关系,即可求出双曲线的离心率.
解答:
解:由题意,|MO|-|MF2|=2a,
∵|OF2|=|F2M|,
∴|OF2|=|F2M|=c,|MO|=2a+c,
∵直线的倾斜角为60°,
∴(2a+c)2=c2+c2-2c•c•cos120°,
∴e2-2e-2=0,
∵e>1,
∴e=
.
故选:B.
∵|OF2|=|F2M|,
∴|OF2|=|F2M|=c,|MO|=2a+c,
∵直线的倾斜角为60°,
∴(2a+c)2=c2+c2-2c•c•cos120°,
∴e2-2e-2=0,
∵e>1,
∴e=
| ||
| 2 |
故选:B.
点评:本题考查双曲线的离心率,考查余弦定理,考查学生的计算能力,确定a,c的关系是关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
如图所示,程序框图(算法流程图)的输出结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
双曲线
-
=1的顶点到渐近线的距离为( )
| x2 |
| 9 |
| y2 |
| 16 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1(a>0,b>0)左、右焦点分别为F1(-c,0),F2(c,0),若双曲线右支上存在点P使得
=
,则该双曲线离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| a |
| sin∠PF1F2 |
| c |
| sin∠PF2F1 |
A、(0,
| ||
B、(
| ||
C、(1,
| ||
D、(
|
已知f(x)=x3-4,则零点一定在( )
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(5,6) |