题目内容
双曲线
-
=1的顶点到渐近线的距离为（ ）
| x2 |
| 9 |
| y2 |
| 16 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：求出双曲线的渐近线方程，顶点坐标，利用点到直线的距离求解即可．
解答：
解：双曲线x2-y2=1的顶点坐标（±3，0），渐近线方程为y=±
x，
所以所求的距离为
=
．
故选：B．
| 4 |
| 3 |
所以所求的距离为
| 4 | ||||
|
| 12 |
| 5 |
故选：B．
点评：本题考查双曲线的简单性质的应用，考查计算能力．
练习册系列答案
相关题目
在每学年学生的评优评先中，某班获得5个推荐名额，其中优秀干部1名，三好生2名，文明生2名，并且三好生和文明生都要求必须有男生参加，班级通过选举定下3男2女共5个推荐对象，则不同推荐方法的种数是（ ）
| A、36 | B、24 | C、22 | D、20 |
C
+2C
+C
等于（ ）
97 98 |
96 98 |
95 98 |
A、C
| ||
B、C
| ||
C、C
| ||
D、C
|
已知y=f（x）是R上的增函数，令F（x）=f（1-x）-f（3+x），则F（x）是R上的（ ）
| A、增函数 | B、减函数 |
| C、先增后减 | D、先减后增 |
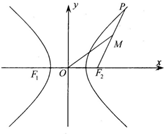如图，双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线的离心率为2，焦点是（6，0），（-6，0），则双曲线的方程为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
过△ABC所在平面α外一点P，作PO⊥α，垂足为O，连接PA，PB，PC．若PA=PB=PC，则点O是△ABC的（ ）
| A、垂心 | B、外心 | C、内心 | D、重心 |