题目内容
若f(x)是定义在R上的奇函数,且满足f(x-2)=-f(x),给出下列4个结论:
①f(2)=0;
②f(x)是以4为周期的函数;
③f(x+2)=f(-x);
④f(x)的图象关于直线x=0对称;
其中所有正确结论的序号是 .
①f(2)=0;
②f(x)是以4为周期的函数;
③f(x+2)=f(-x);
④f(x)的图象关于直线x=0对称;
其中所有正确结论的序号是
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数奇偶性和周期性的性质分别进行判断即可得到结论.
解答:
解:①令x=2,则f(0)=-f(2),则f(2)=-f(0),
∵定义在R上的奇函数f(x),
∴f(0)=0,则f(2)=-f(0)=0,故①正确.
②∵定义在R上的奇函数f(x)满足:f(x-2)=-f(x),
即f(x+2)=-f(x),则f(x+4)=-f(x+2)=f(x),
则函数的周期的定义可以得到:函数f(x)的周期T=4,故②正确;
③②∵定义在R上的奇函数f(x)满足:f(x-2)=-f(x),则f(x)=-f(x+2),
即f(x+2)=-f(x),故③正确.
④∵f(x-2)=-f(x)=f(-x),
∴函数关于x=-1对称,故④错误.
综上正确的命题时①②③,
故答案为:①②③.
∵定义在R上的奇函数f(x),
∴f(0)=0,则f(2)=-f(0)=0,故①正确.
②∵定义在R上的奇函数f(x)满足:f(x-2)=-f(x),
即f(x+2)=-f(x),则f(x+4)=-f(x+2)=f(x),
则函数的周期的定义可以得到:函数f(x)的周期T=4,故②正确;
③②∵定义在R上的奇函数f(x)满足:f(x-2)=-f(x),则f(x)=-f(x+2),
即f(x+2)=-f(x),故③正确.
④∵f(x-2)=-f(x)=f(-x),
∴函数关于x=-1对称,故④错误.
综上正确的命题时①②③,
故答案为:①②③.
点评:此题考查了函数的周期定义及利用定义求函数的周期,还考查了函数的对称及与图象的平移变换,综合考查了函数的性质.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
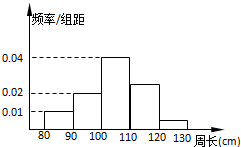 某林业局为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出样本的频率分布直方图(如图),那么估计在这片经济林中,底部周长不小于110cm林木所占百分比为( )
某林业局为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出样本的频率分布直方图(如图),那么估计在这片经济林中,底部周长不小于110cm林木所占百分比为( )| A、70% | B、60% |
| C、40% | D、30% |
用柯西不等式求函数y=
+
+
的最大值为( )
| 2x-3 |
| 2x |
| 7-3x |
A、
| ||
| B、3 | ||
| C、4 | ||
| D、5 |
不等式(x+1)(x-2)<0的解集是( )
| A、(-∞,-2) |
| B、(-2,1) |
| C、(-∞,-1)∪(2,+∞) |
| D、(-1,2) |

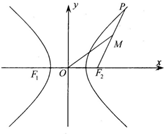 如图,双曲线
如图,双曲线