题目内容
已知f(ex)=x2-2x+3,x∈[2,3]
(1)求f(x)的解析式和定义域;
(2)求f(x)的最大值和最小值.
(1)求f(x)的解析式和定义域;
(2)求f(x)的最大值和最小值.
考点:二次函数在闭区间上的最值,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)首先使用换元法求函数的解析式,进一步求函数的定义域
(2)由(1)的结论,利用函数的单调性求函数的值域.
(2)由(1)的结论,利用函数的单调性求函数的值域.
解答:
解:(1)解:f(ex)=x2-2x+3 ①
设ex=t则x=lnt,代入①式得f(t)=(lnt)2-2lnt+3,
∴f(x)=(lnx)2-2lnx+3,
又x∈[2,3],可得t=ex∈[e2,e3],则函数的定义域:[e2,e3]
(2)由(1)得,x∈[e2,e3],即有lnx∈[2,3],
∴f(x)=(lnx)2-2lnx+3=(lnx-1)2+2,函数f(x)在lnx∈[2,3]是单调递增函数.
当x=e2时,f(x)min=3,
当x=e3时,f(x)max=6,
故答案为:(1)f(x)=(lnx)2-2lnx+3 x∈[e2,e3],
(2)当x=e2时,f(x)min=3;当x=e3时,f(x)max=6.
设ex=t则x=lnt,代入①式得f(t)=(lnt)2-2lnt+3,
∴f(x)=(lnx)2-2lnx+3,
又x∈[2,3],可得t=ex∈[e2,e3],则函数的定义域:[e2,e3]
(2)由(1)得,x∈[e2,e3],即有lnx∈[2,3],
∴f(x)=(lnx)2-2lnx+3=(lnx-1)2+2,函数f(x)在lnx∈[2,3]是单调递增函数.
当x=e2时,f(x)min=3,
当x=e3时,f(x)max=6,
故答案为:(1)f(x)=(lnx)2-2lnx+3 x∈[e2,e3],
(2)当x=e2时,f(x)min=3;当x=e3时,f(x)max=6.
点评:本题考查的知识点:换元法在求解析式中的应用,求函数的定义域,利用函数的单调性进行求函数的值域及相关的运算.

练习册系列答案
相关题目
若直线x+y+a=0过圆x2+y2-2x+4y=0的圆心,则a的值为( )
| A、0 | B、-1 | C、2 | D、1 |
 执行如图所示的程序框图,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出数对(x,y)的概率为( )
执行如图所示的程序框图,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出数对(x,y)的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,已知M是BC中点,设
=
,
=
,则
=( )
| CB |
| a |
| CA |
| b |
| AM |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
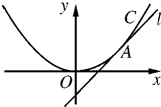 如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.
如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.